Exercice sur les polynômes

par **Epsilon** » 23 Jan 2010, 10:57

pour quel valeur de

le polynôme

est divisible par

?
ce que j'ai fait:

aider moi , merci

par **girdav** » 23 Jan 2010, 11:02

Regarde les racines de

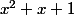
et regarde si elle sont racines de

.

par **Doraki** » 23 Jan 2010, 11:06

Là tu vas droit dans le mur.

Remarque que (x²+x+1) divise (x^3 - 1) ainsi que (x+1)² - x
Ca devrait te permettre de simplifier un peu le problème.

par **Epsilon** » 23 Jan 2010, 11:13

svp expliquer encore une fois , que ce que je doit remarquer ? !

par **girdav** » 23 Jan 2010, 11:20

Que veut dire "Le polynôme

divise le polynôme

?

par **Ben314** » 23 Jan 2010, 11:22

A mon avis, la méthode la plus "standard" est celle proposée par girdav (celle de doraki est plus "astucieuse")
Je pense que tu as vu que :
Un polynôme P divise un polynôme Q ssi toutes les racines de P (dans C) sont des racines de Q [avec un ordre de multiplicité supérieur ou égal]

par **Epsilon** » 23 Jan 2010, 12:27

Ben314 a écrit:A mon avis, la méthode la plus "standard" est celle proposée par girdav (celle de doraki est plus "astucieuse")
Je pense que tu as vu que :
Un polynôme P divise un polynôme Q ssi toutes les racines de P (dans C) sont des racines de Q [avec un ordre de multiplicité supérieur ou égal]

euh,j'ai devant moi un cours de cryptographie , et il n ya pas ce résultat !

donc je doit voir une condiction sur les racines des deux polynômes ?

Exercice sur les polynômes

exercice sur les polynômes

Qui est en ligne