Exercice sur les polynomes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
par valsad » 02 Juil 2010, 16:29
Bonjour,
Je travaille actuellement sur les polynômes et j'ai des difficultés pour résoudre un exercice:
Soient les polynômes Pn et Qn définis par :
=(1+\frac{X}{2n+1})^{2n+1}-(1-\frac{X}{2n+1})^{2n+1})
et
=(1+X)^{2n+1}-(1-X)^{2n+1})
1) Résoudre dans C
^{2n+1}=(1-u)^{2n+1})
=>
avec
2)Montrer que :
=2u\prod_{p=1}^n \left(u^2 + \tan^2 \left(\frac{p\pi}{2n+1}\right)\right))
puis que:
=2(2n+1)u\prod_{p=1}^n \left(1+\frac{u^2}{ \tan^2 \left(\frac{p\pi}{2n+1}\right)}\right))
=>Pour cette question, je ne sais pas du tout comment faire!!!
3)En déduire une factorisation de Pn.
=> je n'y ai pas encore réfléchi.
Quelqu'un peut m'aider pour la question 2) svp?
Merci d'avance.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 02 Juil 2010, 16:40
On sait que
est à coefficients réels. On regroupe une racine avec son conjugué.
Si
est racine, que dire de
?
Que donne
\(z-\bar u\))
?
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
par valsad » 02 Juil 2010, 17:28
si u est racine de Qn =>
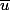
est racine de Qn aussi
(z-\bar{u})=z^2-2zRe(u)+\mid{u}\mid^2)
et si je calcule
avec
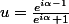
, je trouve:
)
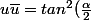Ce qui est très intéressant pour trouver le résultat...
Mais je suis toujours bloquée!!!
Pouvez-vous m'aider encore un peu svp?
Merci.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 02 Juil 2010, 18:25
Bon, il ne te reste plus qu'à calculer
. On peut écrire que
.
-
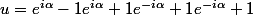
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
par Sa Majesté » 02 Juil 2010, 18:55
Sinon on peut s'en sortir avec
}{2 \cos \left(\frac{k\pi}{2n+1}\right)} = i \tan \left(\frac{k\pi}{2n+1}\right))
D'où
 = \alpha \prod_{k=0}^{2n} \left(X-i \tan \left(\frac{k\pi}{2n+1}\right)\right))
Et on regroupe les facteurs conjugués
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 02 Juil 2010, 19:34
Sa Majesté a écrit:Sinon on peut s'en sortir avec
D'où
Et on regroupe les facteurs conjugués
Le coefficient dominant est
et non
.
-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
par Sa Majesté » 02 Juil 2010, 19:37
girdav a écrit:Le coefficient dominant est
et non
.
Bien sûr que c'est 2 mais il faut le montrer dans un 2ème temps
Avec la variante que j'ai proposée on ne peut pas encore conclure que c'est 2
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 02 Juil 2010, 19:40
Sa Majesté a écrit:Bien sûr que c'est 2 mais il faut le montrer dans un 2ème temps
Avec la variante que j'ai proposée on ne peut pas encore conclure que c'est 2
Ce qui m'a induit en erreur est que vous avez appelé le coefficient dominant
comme dans l'écriture de
.
-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
par Sa Majesté » 02 Juil 2010, 19:43
girdav a écrit:Ce qui m'a induit en erreur est que vous avez appelé le coefficient dominant
comme dans l'écriture de
.
Ah OK mes excuses je n'avais pas compris la confusion (qui est légitime) :happy2:
J'aurais dû écrire
alors :zen:
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
par valsad » 02 Juil 2010, 22:28
Merci beaucoup pour vos aides! j'ai pu retrouver l'expression demandée sauf pour le coefficient 2. Faut-il prendre une valeur particulière pour le retrouver? comme
)
?
Merci encore.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 02 Juil 2010, 23:12
Ca risque de marcher, mais, pour la première égalité de la question 2), il serait plus simple d'utiliser le fait que le coeff. dominant (i.e. celui en
) de
=(1+X)^{2n+1}-(1-X)^{2n+1})
est
^{2n+1}=2)
.
Pour la deuxième égalité de cette même question, tu as intérêt à évaluer le coeff en X de
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
valsad
- Membre Naturel
- Messages: 73
- Enregistré le: 17 Sep 2009, 08:23
-
par valsad » 03 Juil 2010, 17:11
Merci! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
