Ben314 a écrit:Vu le résultat que tu trouve, il semblerais que tu ait fait un peu compliqué : en fait "l'astuce", c'est de voir que

vérifie
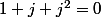
donc
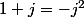
(qui est racine 6em de l'unité).
Oui j'ai la mauvaise manie de compliqué les choses en maths^^
Ben314 a écrit:Donc
=aj+b=(j+1)^n-j^n-1=(-1)^nj^{2n}-j^n-1)
et le résultat dépénd uniquement du reste

de la division euclidienne de

par 6 : il y a donc uniquement 6 restes possibles...
J'ai utilisé cette égalité... pour aboutir à mon résultat compliqué...
Finalement j'ai procéder autrement, mais il y a trop de distinctions de cas à mon goût :
-Supposons
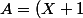^n-X^n-1)
est divisible par
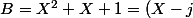(X-j^2))
(où
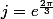
est une racine 3-ème de l'unité)
Alors

(et

) sont racines de A
Je distingue deux cas :
--Cas où

est pair :
alors on a
=0)
, soit
^n-j^n-1=0)
d'où
^n-j^n-1=0)
or
^n-j^n-1=(e^{\frac{4\pi}{3}})^n-e^{\frac{2n\pi}{3}}-1=e^{\frac{-2n\pi}{3}}-e^{\frac{2n\pi}{3}}-1=-2i \times sin(\frac{2n\pi}{3})-1\neq0)
donc le cas n pair n'est pas possible.
--

ne peut être qu'impair, dans ce cas :
^n-j^n-1=-(e^{\frac{4\pi}{3}})^n-e^{\frac{2n\pi}{3}}-1=-e^{\frac{-2n\pi}{3}}-e^{\frac{2n\pi}{3}}-1=-(2cos(\frac{2n\pi}{3})+1))
or
+1=0)
si et seulement si
= - \frac{1}{2})
,
c'est-à dire, ssi il existe
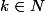
tel que
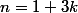
ou
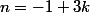
(k doit être nécessairement pair et positif car n est impair et positif)
donc ssi

est congru à 1 ou à 2 modulo 3
-Inversement, si

est impair et congru à 1 ou à 2 modulo 3, on montre bien que

et

sont racines de

(en tout cas j'ai réussi à le montrer après quelques calculs)
J'en conclus que

est divisible par

pour tous entiers naturels impairs

congru à 1 ou à 2 modulo 3
Perso, je trouve que ce que j'ai fait est bien trop long, je n'arrive pas à trouver une méthode plus fine et astucieuse (j'ai essayé de faire avec ce que tu as proposé, mais j'ai pas vraiment compris en fait...)
