Exercice de révision,entrainement sur les complexes
12 messages
- Page 1 sur 1
Exercice de révision,entrainement sur les complexes
Bonjour à tous, j'envoi cet exercice car j'ai essayé de faire cet exercice, quelqu'un pourrai-t-il corrigé les éventuelles erreurs svp? (la question 3 j'ai pas compris).
https://zupimages.net/viewer.php?id=23/04/h62s.png
https://zupimages.net/viewer.php?id=23/04/h62s.png
Re: Exercice de révision,entrainement sur les complexes
Bonjour,
connais-tu la forme exponentielle ?
Z=1-iV3 est juste.
On pouvait alors dire :
Z=2(1/2-iV/2)= 2(cos(-pi/3)+i sin(-pi/3), réponse juste que tu as trouvée et qui s'écrit aussi :
Z= 2 e^(-ipi/3)
Donc :
Z^3= 8 e(-ipi)=-8
Pour Z^3, je ne comprend pas ta puissance 8.
connais-tu la forme exponentielle ?
Z=1-iV3 est juste.
On pouvait alors dire :
Z=2(1/2-iV/2)= 2(cos(-pi/3)+i sin(-pi/3), réponse juste que tu as trouvée et qui s'écrit aussi :
Z= 2 e^(-ipi/3)
Donc :
Z^3= 8 e(-ipi)=-8
Pour Z^3, je ne comprend pas ta puissance 8.
Re: Exercice de révision,entrainement sur les complexes
bonjour,
question 2
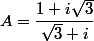
On multiplie haut et bas par le conjugué du dénominateur:
(\sqrt{3}-i)}{4})
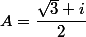
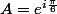 (1er quadrant du cercle trigonométrique)
(1er quadrant du cercle trigonométrique)
question 2
On multiplie haut et bas par le conjugué du dénominateur:
Re: Exercice de révision,entrainement sur les complexes
Question 3
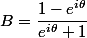
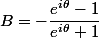
mettre en facteur en haut et en bas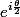
sachant que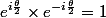
je te laisse démontrer que le résultat de l'énoncé concernant la question 3 est faux.
mettre en facteur en haut et en bas
sachant que
je te laisse démontrer que le résultat de l'énoncé concernant la question 3 est faux.
Modifié en dernier par mathelot le 23 Jan 2023, 16:36, modifié 1 fois.
Re: Exercice de révision,entrainement sur les complexes
Bonjour
Juste une remarque pour la question 2, parfois il n'est pas facile de passer de la forme algébrique finale à la forme trigonométrique.
Dans ce cas on cherche les formes exponentielles des deux termes du quotient puis on effectue la division grâce aux formules connues.
Plus clairement
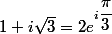
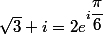
D'où le quotient :}=e^{i\dfrac{\pi}{6})
Cela peut être utile si par exemple on a 1+i au dénominateur (sans changer le numérateur), 1+i est d'argument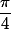 donc le quotient aurait pour argument
donc le quotient aurait pour argument 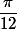 ce qui n'est pas facile à trouver à partir de la forme algébrique.
ce qui n'est pas facile à trouver à partir de la forme algébrique.
Juste une remarque pour la question 2, parfois il n'est pas facile de passer de la forme algébrique finale à la forme trigonométrique.
Dans ce cas on cherche les formes exponentielles des deux termes du quotient puis on effectue la division grâce aux formules connues.
Plus clairement
D'où le quotient :
Cela peut être utile si par exemple on a 1+i au dénominateur (sans changer le numérateur), 1+i est d'argument
Re: Exercice de révision,entrainement sur les complexes
mathelot a écrit:Question 3
mettre en facteur en haut et en bas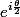
sachant que
je te laisse démontrer que le résultat de l'énoncé concernant la question 3 est faux.
Merci beaucoup, pour la question 2 j'avais un doute
Re: Exercice de révision,entrainement sur les complexes
catamat a écrit:Bonjour
Juste une remarque pour la question 2, parfois il n'est pas facile de passer de la forme algébrique finale à la forme trigonométrique.
Dans ce cas on cherche les formes exponentielles des deux termes du quotient puis on effectue la division grâce aux formules connues.
Plus clairement
D'où le quotient :
Cela peut être utile si par exemple on a 1+i au dénominateur (sans changer le numérateur), 1+i est d'argumentdonc le quotient aurait pour argument
ce qui n'est pas facile à trouver à partir de la forme algébrique.
Je n'avais jamais vu ça comme, ça, soit il faut connaitre quelques forme trigonométrique, soit il faut les trouvé séparément , puis divisé comme tu l'a fait, c'est malin merci

Re: Exercice de révision,entrainement sur les complexes
Françoisdesantilles a écrit:mathelot a écrit:Question 3
mettre en facteur en haut et en bas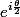
sachant que
je te laisse démontrer que le résultat de l'énoncé concernant la question 3 est faux.
Merci beaucoup, pour la question 2 j'avais un doute
factorise
Re: Exercice de révision,entrainement sur les complexes
re,
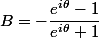
}{e^{i \frac{\theta}{2}}(e^{i\frac{\theta}{2}}+e^{-i\frac{\theta}{2}})})
}{2 \cos(\frac{\theta}{2})})
 e^{i \pi})
Modifié en dernier par mathelot le 28 Jan 2023, 15:25, modifié 1 fois.
Re: Exercice de révision,entrainement sur les complexes
Bonjour,
@Françoisdesantilles
si tu ne connais pas la technique de l'angle moitié, tu peux aussi procéder ainsi:
-i\, sin(\theta)}{1+cos(\theta)+i\,sin(\theta)})
\left[sin(\dfrac{\theta}{2})-i\,cos(\dfrac{\theta}{2})\right]}{ cos(\dfrac{\theta}{2})\left[cos(\dfrac{\theta}{2})+i\,sin(\dfrac{\theta}{2})\right]}=\dfrac{-i\,sin(\dfrac{\theta}{2})\left[cos(\dfrac{\theta}{2})-\dfrac{1}{i}\,sin(\dfrac{\theta}{2})\right]}{ cos(\dfrac{\theta}{2})\left[cos(\dfrac{\theta}{2})+i\,sin(\dfrac{\theta}{2})\right]}=\dfrac{-i\,sin(\dfrac{\theta}{2})\left[cos(\dfrac{\theta}{2})+i\,sin(\dfrac{\theta}{2})\right]}{ cos(\dfrac{\theta}{2})\left[cos(\dfrac{\theta}{2})+i\,sin(\dfrac{\theta}{2})\right]})
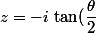)
mais il est préférable d'utiliser la technique de l'angle moitié
attention quand même : n'oublie pas de vérifier que le dénominateur+i sin(\theta)) est différent de 0
est différent de 0
@Françoisdesantilles
si tu ne connais pas la technique de l'angle moitié, tu peux aussi procéder ainsi:
mais il est préférable d'utiliser la technique de l'angle moitié
attention quand même : n'oublie pas de vérifier que le dénominateur
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
