Hello, j'essaie de faire l'exercice suivant
Soit
_{1\leq i,j\leq n})
avec
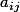
des variables aléatoires indépendantes entre elles et de même loi uniforme sur
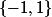
. Calculer
))
et
))
.
Le premier calcul se fait très bien avec la grosse formule
=\sum_{\sigma\in S_n}\varepsilon(\sigma)a_{1\sigma(1)}\cdots a_{n\sigma(n)}.)
On trouve
ce qui est assez logique. Pour le deuxième calcul je trouve des résultats différents en fonction de la méthode que j'emploie. Aucune des méthodes ne donne le même résultat et pire : aucune ne coïncide avec les simulations. L'idée que j'ai eu est de réutiliser la grosse formule pour calculer
))
avec
)
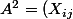et
. J'ai montré le lemme suivant
Soient
trois variables aléatoires de loi uniforme sur
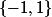
avec
indépendante de
et de
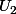
alors
et
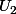
sont indépendantes de même loi uniforme sur
.
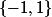
Ceci montre que lorsque
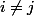
les
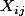
sont des sommes d'uniformes sur
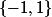
et qu'elles sont indépendantes de
pour tout
)
. On en déduit alors que le seul terme restant dans la grosse formule est celui correspondant à l'identité donc que
)=E(X_{11}\cdots X_{nn}))
En poursuivant le calcul il s'agit du nombre d'involutions de
En faisant la même chose mais en calculant
)
j'arrive à un résultat différent qui est
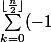^k n^{n-k}\sum_{j=1}^k \binom{n-2j}{2})
car les seuls termes restants sont ceux correspondant aux permutations involutives grâce au fait que ce coup ci
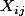
est indépendant des autres coefficients à part
. Cette formule est pour le coup assurément fausse car donne 0 pour
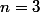
et
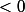
pour
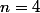
ce qui n'est vraiment pas terrible pour l'espérance d'une variable aléatoire positive prenant des valeurs strictement positives.
Je crois que mon erreur provient de ma conclusion :
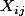
indépendante de
pour tout
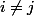
et pour tout
. Mais je ne vois pas où est l'erreur dans cette conclusion...
Les simulations semblent indiquer que le bon résultat est
. Voir le code magma
https://magma.maths.usyd.edu.au/calc/ ci-dessous.
- Code: Tout sélectionner
n:=3;
MF2:=KMatrixSpace(Integers(2),n,n);
S := {Matrix(Integers(),n,n,[[2*Integers()!x-1 : x in Eltseq(y)] : y in Rows(M)]) : M in MF2 };
v := 0;
for M in S do
v +:= Determinant(M)^2;
end for;
v/2^(n^2);
.