Exercice-Fracions rationnelles

[Easyblue]

Bonjour!

J'ai un exercice sur les fractions rationnelles à résoudre (niveau iufm de maths) et je suis complètement larguée.
Le but de l'exercice est de résoudre le système d'équations suivant:
pour tout i dans [0,2n-1] somme (pour k=1 à n) des (x indice k) * ((y indice k) à la puissance i)= a indice i
Si quelqu'un à fait un exercice du même genre ou si cette personne peut m'expliquer comment résoudre ce système (en se ramenant à la résolution d'unsystème linéaire suivie de la décomposition en éléments simples d'une fraction rationnelle) merci de bien vouloir répondre à mon message.

[Zebulon]

Bonsoir,
pour l'instant je vois qu'on peut écrire ce système matriciellement :

mais ensuite, pour résoudre, quelles sont les inconnues et quelles sont les données ?

[Easyblue]

Bonsoir,
pour l'instant je vois qu'on peut écrire ce système matriciellement :

mais ensuite, pour résoudre, quelles sont les inconnues et quelles sont les données ?

Peux-tu me dire comment tu fais pour écrire les écriture mathématiques se seraient plus simple pour moi de te donner les données.
Sinon les inconnues sont les x et les y avec leurs inedinces évidemment.

[Zebulon]

J'ai oublié la puissance 0. C'est donc :

La matrice de droite (les ) me fait penser à un déterminant de Vandermonde, donc on sait à quelle condition c'est inversible, mais je ne sais pas trouver l'inverse...

[Zebulon]

Peux-tu me dire comment tu fais pour écrire les écriture mathématiques se seraient plus simple pour moi de te donner les données.

J'utilise TEX :
http://fr.wikipedia.org/wiki/Aide:Formules_TeX.

[Zebulon]

La matrice de droite (les ) me fait penser à un déterminant de Vandermonde

Je dis des bêtises, cette matrice n'est même pas carrée...

[Easyblue]

Je dis des bêtises, cette matrice n'est même pas carrée...

On ramène cette résolution à la résolution d'un système linéaire suivie de la décomposition en éléments simples d'une fraction rationnelle.
Question 1:
Montrer que (T) = =()/()
est égal à

Ca c'est fait.
Question 2:
En déduire un système de n+1 équations linéaires à n+1 inconnues dont les solutions sont les et en déduire le calcul des
Question 3:
Expliquer comment on peut résoudre alors le système de départ

Désolé pour le TEX je maîtrise pas....

[Zebulon]

Pour TeX, j'ai l'impression que vous avez tout bien tapé, mais il faut mettre entre balises TeX pour que ça s'affiche ! :ptdr:
Vous surlignez et vous cliquez sur TeX, en haut à droite du texte.

[Easyblue]

Pour TeX, j'ai l'impression que vous avez tout bien tapé, mais il faut mettre entre balises TeX pour que ça s'affiche ! :ptdr:
Vous surlignez et vous cliquez sur TeX, en haut à droite du texte.

C'est mieux, non?

[Easyblue]

C'est mieux, non?

S'il vous plaît, aidez moi!!!!!!!!!!!!!!!!!!!!!!!

[Quidam]

Je refais la première question, histoire de vérifier que l'on est bien en phase tous les deux...

Je pars de la formule :

Si j'ai bien compris, c'est ça une série formelle !

Alors :








...en posant :


Et comme tes équations de départ s'écrivent :
,


Par ailleurs, comme tu l'as écrit, on peut dire que :
, les et étant des coefficients.
On a donc :

En multipliant les deux membres par : , j'obtiens alors :


En identifiant les 2n premiers coefficients, pour i=0 à 2n-1, respectivement des monômes de degré i de part et d'autre du signe "=", j'obtiens (2n) équations linéaires avec les 2n inconnues , i=1 à n, et , j=1 à n, ce qui me permet de les trouver !
Enfin, la connaissance de ces coefficients me permet de décomposer la fraction rationnelle en éléments simples et de trouver les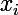 et les

J'espère que je n'ai pas dit trop de bêtises : je ne suis vraiment pas familier avec les séries formelles !

[Easyblue]

Je refais la première question, histoire de vérifier que l'on est bien en phase tous les deux...

Je pars de la formule :

Si j'ai bien compris, c'est ça une série formelle !

Alors :








...en posant :


Et comme tes équations de départ s'écrivent :
,


Par ailleurs, comme tu l'as écrit, on peut dire que :
, les et étant des coefficients.
On a donc :

En multipliant les deux membres par : , j'obtiens alors :


En identifiant les 2n premiers coefficients, pour i=0 à 2n-1, respectivement des monômes de degré i de part et d'autre du signe "=", j'obtiens (2n) équations linéaires avec les 2n inconnues , i=1 à n, et , j=1 à n, ce qui me permet de les trouver !
Enfin, la connaissance de ces coefficients me permet de décomposer la fraction rationnelle en éléments simples et de trouver les et les

J'espère que je n'ai pas dit trop de bêtises : je ne suis vraiment pas familier avec les séries formelles !

Tu n'as pas dis de bêtises mise à part peut-être que tu as 2n équations et qu'on ne nous en demande que n+1.
J'étais aussi arrivée jusqu'ici.
Mon problème en fait c'est que je n'arrive pas à calculer les et .

[Quidam]

Tu n'as pas dis de bêtises mise à part peut-être que tu as 2n équations et qu'on ne nous en demande que n+1.
J'étais aussi arrivée jusqu'ici.
Mon problème en fait c'est que je n'arrive pas à calculer les et .

Oui, tu as raison, ya un truc qui cloche ! Au départ, on a 2n équations et 2n inconnues. Le problème est qu'à présent on a 2n+1 inconnues : les , pour i=0 à n-1 et les , pour j=0 à n !!!! Va falloir ruser :ruse: !

Cependant, tu remarqueras que dans ces 2n équations, celles qui concernent les coefficient n à 2n-1 (soit n) équations, ne font pas intervenir les : certes, il en manque une pour trouver les (n+1) valeurs Donc, une fois qu'on aura trouvé l'équation qui nous manque (:mur:), on pourra effectivement trouver dans un premier temps les (n+1) , et dans un deuxième temps, les (n) .
Je cherche... :doute2:

[Easyblue]

Oui, tu as raison, ya un truc qui cloche ! Au départ, on a 2n équations et 2n inconnues. Le problème est qu'à présent on a 2n+1 inconnues : les , pour i=0 à n-1 et les , pour j=0 à n !!!! Va falloir ruser :ruse: !

Cependant, tu remarqueras que dans ces 2n équations, celles qui concernent les coefficient n à 2n-1 (soit n) équations, ne font pas intervenir les : certes, il en manque une pour trouver les (n+1) valeurs Donc, une fois qu'on aura trouvé l'équation qui nous manque (:mur:), on pourra effectivement trouver dans un premier temps les (n+1) , et dans un deuxième temps, les (n) .
Je cherche... :doute2:

C'est vrai qu'on peut dire qu'il manque une équation pour les mais on devine d'après l'énoncé que .

[Quidam]

C'est vrai qu'on peut dire qu'il manque une équation pour les mais on devine d'après l'énoncé que .

Bon sang, mais c'est bien sûr !
Les (2n+1) inconnues , i=0 à n-1 et , j=0 à n, ne sont définies qu'à un facteur près ! Car si :

Alors, si on définit et , avec k non nul, on a également :


Il faut donc ajouter une équation, par exemple , mais on peut aussi prendre ou . Mais il faut prendre garde qu'il est possible que les solutions du système à n+1 inconnues et seulement n équations peuvent avoir toutes la caractéristique que (parce que !).

En toute rigueur, si l'on n'avait pas d'indication supplémentaire sur , il faudrait résoudre "proprement" le système linéaire de n équations à (n+1) inconnues, ce qui doit nous fournir une infinité de solutions du type , j=0 à n, et choisir une valeur simple de k non nulle (pas forcément 1, ça peut par exemple être le dénominateur commun aux , pour avoir des expressions plus simples), ce qui n'exclut pas "a priori" la valeur 0 pour

Mais justement, il est clair que ne peut pas être nul, d'après sa définition ! On peut donc tout simplement ajouter l'équation qui sera notre (n+1)-ième équation !