Exercice disparu

[yos]

Il y avait hier un joli exercice de probabilités que je ne trouve plus. Aurait-il été modéré par un modérateur immodéré?

Pour une partie E de , on pose
.
Lorsque cette suite converge, on note f(E) sa limite.

Il y avait une première question dont le sens m'échappe mais la seconde est intéressante :

trouver deux parties et telles que et existent mais n'existe pas.

Fabriquer une partie E pour laquelle f(E) n'existe pas demande déjà un peu de réflexion. L'écrire comme intersection de deux parties dont les suites converge ne me semble pas du tout évident.

[Dyo]

E est nécessairement fixé ?

Sinon pour le 1er, on aurait pu dire :

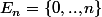
si pair, si impair ?

[yos]

Oui, E est fixé.
Pour chaque ensemble E, tu as une suite
On a toujours .

Si E est fini, tend clairement vers 0.
Si E est l'ensemble des entiers pairs, converge vers 1/2.

[leon1789]

représente une espèce de "densité" de E dans N.

Imaginons
Alors diverge (car oscille de plus en plus lentement entre 1/3 et 2/3).

[leon1789]

Ensuite, pour trouver des E1 et E2 , on peut peut-être
prendre où est strictement croissante.
puis E1 = E union {les nombres impairs} et E2 = E union {les nombres pairs} ??????