Exercice calcul de somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 06 Sep 2013, 17:06
par lopilu » 06 Sep 2013, 17:06
Bonjour, je bloque sur un exercice et je viens vous demander votre aide car je n'en peux vraiment plus !
Voici l'exercice :

n


*, on note Sn=

1. a. Justifier que

n


* - {1},
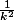


-
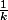
b. En déduire que

n


*, Sn

2-

c. En déduire que la suite (Sn) est majorée.
2. Déterminer le sens de variation de la suite (Sn).
3. En déduire que la suite (Sn) est convergente.
Merci infiniment pour votre aide ! :we:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 06 Sep 2013, 17:36
par capitaine nuggets » 06 Sep 2013, 17:36
Salut !
lopilu a écrit:Bonjour, je bloque sur un exercice et je viens vous demander votre aide car je n'en peux vraiment plus !
Voici l'exercice :

n


*, on note Sn=

1. a. Justifier que

n


* - {1},
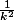


-
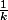
b. En déduire que

n


*, Sn

2-

c. En déduire que la suite (Sn) est majorée.
2. Déterminer le sens de variation de la suite (Sn).
3. En déduire que la suite (Sn) est convergente.
Merci infiniment pour votre aide ! :we:
Où bloques-tu ?
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 06 Sep 2013, 17:38
par lopilu » 06 Sep 2013, 17:38
En effet j'ai oublié de préciser où je bloquais. En réalité je bloque dès la première question, après de multiples essais et méthodes. Mais pour la 1.b j'ai une vague idée de comment faire, et la suite c'est légèrement le flou...

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 06 Sep 2013, 17:44
par capitaine nuggets » 06 Sep 2013, 17:44
1°)a) Pour
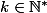
,

donc
\le k^2)
.
Par passage à l'inverse...
b) L'application

est strictement décroissante sur

donc l'ensemble des majorants est...
c) Il faut réunir les deux conditions précédentes : ... et ...
2°)

donc tu en déduis le signe de
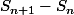
.
3°) Sers-toi des questions 1°)c) et 2°)
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 06 Sep 2013, 17:49
par lopilu » 06 Sep 2013, 17:49
C'est génial ! Merci beaucoup, je me met tout de suite au travail !
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 06 Sep 2013, 18:13
par Archibald » 06 Sep 2013, 18:13
Ou sinon,
a) on remarque que :
}{(k-1)k} \ = \ \frac{1}{k^2-k} \ \gt \quad \frac{1}{k^2})
b) Sn série géométrique de raison 1/2, d'où :
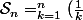^2 \ = \ \frac{1-(1/2)^{n+1}}{1-(1/2)} \ = \ 2-(1/2)^n \ = \ \cdots)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 06 Sep 2013, 19:07
par capitaine nuggets » 06 Sep 2013, 19:07
Archibald a écrit: Sn série géométrique de raison 1/2, d'où :
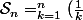^2 \ = \ \frac{1-(1/2)^{n+1}}{1-(1/2)} \ = \ 2-(1/2)^n \ = \ \cdots)
C'est excessivement faux ce que tu dis !

n'est certainement pas une série géométrique :hum:
Déjà, c'est une
somme partielle associée à la série :
[CENTER]

[/CENTER]
dite de Riemann (d'ordre 2) convergeant vers

.
Cela impliquerait l'existence d'un rang

, à partir duquel quel que soit
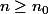
,

.
Or ce n'est pas le cas.
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 06 Sep 2013, 19:31
par Archibald » 06 Sep 2013, 19:31
Tu remarqueras que j'ai lu
^2)
en lieu et place de
^2)
(allez savoir pourquoi) donc il y a déjà un couac. Le reste n'est qu'abus de langage de ma part, ça m'apprendra à être plus rigoureux dans ma rédaction la prochaine fois.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Sep 2013, 19:32
par deltab » 06 Sep 2013, 19:32
Bonsoir
Pour la majoration

, essaies d'utiliser la suite
)
en simplifiant éventuellement son expression (somme télescopique).

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 06 Sep 2013, 19:35
par capitaine nuggets » 06 Sep 2013, 19:35
Archibald a écrit:Tu remarqueras que j'ai lu
^2)
en lieu et place de
^2)
(allez savoir pourquoi) donc il y a déjà un couac. Le reste n'est qu'abus de langage de ma part, ça m'apprendra à être plus rigoureux dans ma rédaction la prochaine fois.
Pas de problème :++:
Je me disais aussi que ça me semblait bizarre venant de toi mais te voyant poursuivre je me suis dit que t'avais rien remarqué :+++:
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 09 Sep 2013, 20:39
par lopilu » 09 Sep 2013, 20:39
Après avoir expérimenté plusieurs de vos techniques durant plusieurs jours, je n'arrive toujours pas à la fin de cette exercice, ne trouvant jamais les bons résultats et bonnes équations...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Sep 2013, 20:41
par leon1789 » 09 Sep 2013, 20:41
As-tu prouvé que (Sn) est majorée ?
As-tu prouvé que (Sn) est croissante ?
Maintenant, il y a un théorème qui prouve que (Sn) converge, non ?
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 09 Sep 2013, 20:44
par lopilu » 09 Sep 2013, 20:44
Je bloque à la question précédente, où il faut prouver l'inégalité.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Sep 2013, 20:46
par leon1789 » 09 Sep 2013, 20:46
lopilu a écrit:Je bloque à la question précédente, où il faut prouver l'inégalité.

Pour k>1, tu as prouvé

donc

ok ?
Et puis

ok ?
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 09 Sep 2013, 20:51
par lopilu » 09 Sep 2013, 20:51
C'est ici que j'avais un problème, j'avais oublié justement le +1 en changeant les bornes de Sn. Erreur stupide d'étourderie, ne m'en dis pas plus, je vais essayer maintenant et ça devrait beaucoup mieux aller. Merci beaucoup de ton aide !
-
Archibald
- Membre Relatif
- Messages: 415
- Enregistré le: 05 Avr 2013, 17:06
-
 par Archibald » 09 Sep 2013, 21:09
par Archibald » 09 Sep 2013, 21:09
Au passage, je viens de remarquer une erreur de capitaine nuggets :
capitaine nuggets a écrit:b) L'application

est strictement
décroissante sur

donc l'ensemble des majorants est...
sans rancune ^^
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 09 Sep 2013, 21:42
par lopilu » 09 Sep 2013, 21:42
Donc si je comprends bien pour la suite de l'exercice : pour montrer qu'elle est majorée, j'utilise les deux éléments que j'ai démontré précédemment. Pour déterminer son sens de variation et montrer qu'elle converge, j'étudie son signe en faisant la différence Sn+1 - Sn, mais n'est-ce pas un peu long de devoir faire cette différence de somme ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 09 Sep 2013, 21:51
par leon1789 » 09 Sep 2013, 21:51
lopilu a écrit: Pour déterminer son sens de variation et montrer qu'elle converge, j'étudie son signe en faisant la différence Sn+1 - Sn, mais n'est-ce pas un peu long de devoir faire cette différence de somme ?
ben non, c'est pas long, c'est instantané !
regarde les sommes : ce sont les mêmes sauf la borne supérieure...
Sn+1 - Sn = 1/(...)^2
-
lopilu
- Membre Naturel
- Messages: 65
- Enregistré le: 16 Oct 2011, 16:43
-
 par lopilu » 09 Sep 2013, 22:03
par lopilu » 09 Sep 2013, 22:03
Je pensais que c'était plus long et voyait cela plus compliqué... Je mexécute tout de suite à le faire, même si ce sera un peu long vu l'heure !
En tout cas merci beaucoup pour l'aide !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
n

*, on note Sn=
n

* - {1},
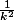

-
n

*, Sn
2-

en lieu et place de
(allez savoir pourquoi) donc il y a déjà un couac. Le reste n'est qu'abus de langage de ma part, ça m'apprendra à être plus rigoureux dans ma rédaction la prochaine fois.