Evn, fermés
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 22 Oct 2012, 22:11
par Supernova » 22 Oct 2012, 22:11
cet ensemble est compact?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 23 Oct 2012, 09:53
par arnaud32 » 23 Oct 2012, 09:53
Supernova a écrit:Holà!
Je veut mq l'ensemble des projecteurs de E (supposé de dim finie) est fermé.
Avec quelle norme dois-je travailler? Et quelle propriété pourrais-je montrer pour que p (supposé être la limite d'une suite de proj de E) soit un projecteur?
Merci
quelle topologie utilises tu pour l'ensemble des projecteurs?
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 23 Oct 2012, 21:46
par Supernova » 23 Oct 2012, 21:46
arnaud32 a écrit:quelle topologie utilises tu pour l'ensemble des projecteurs?
Aucune idée, c'est pas indiqué dans l'exo
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Oct 2012, 09:25
par arnaud32 » 24 Oct 2012, 09:25
Supernova a écrit:Aucune idée, c'est pas indiqué dans l'exo
je suppose que tu te places sur L(E,E) muni de la norme |||.||| ?
dans ce cas ca que tu veux monter c'est que si
_{n \in \mathbb{N}})
est une suie de projecteurs qui converge vers u dans L(E,E) alors u est un projecteur
tu vas regarder uou-u
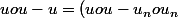 +(u_nou_n-u_n) + (u_n-u))
tuas aussi
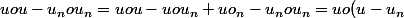+(u-u_n)ou_n)

car

est un projecteur
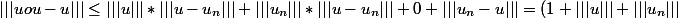*|||u-u_n|||)
etc ...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 24 Oct 2012, 12:14
par Doraki » 24 Oct 2012, 12:14
Supernova a écrit:cet ensemble est compact?
En utilisant la norme triple (L(E) est de dimension finie, à savoir n², donc elles sont toutes équivalentes), est-ce que cet ensemble est borné ?
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 24 Oct 2012, 20:33
par Supernova » 24 Oct 2012, 20:33
Doraki a écrit:En utilisant la norme triple (L(E) est de dimension finie, à savoir n², donc elles sont toutes équivalentes), est-ce que cet ensemble est borné ?
Nn il n'est pas borné
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 24 Oct 2012, 20:39
par Supernova » 24 Oct 2012, 20:39
arnaud32 a écrit:je suppose que tu te places sur L(E,E) muni de la norme |||.||| ?
dans ce cas ca que tu veux monter c'est que si
_{n \in \mathbb{N}})
est une suie de projecteurs qui converge vers u dans L(E,E) alors u est un projecteur
tu vas regarder uou-u
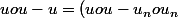 +(u_nou_n-u_n) + (u_n-u))
tuas aussi
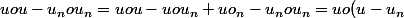+(u-u_n)ou_n)

car

est un projecteur
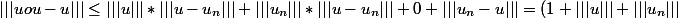*|||u-u_n|||)
etc ...
Voilà une autre méthode pour mq l'ensemble des projecteurs est fermé, en passant à la limite dans la dernière inégalité on obtient le résultat, merci

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Oct 2012, 00:30
par Doraki » 25 Oct 2012, 00:30
Supernova a écrit:Nn il n'est pas borné
Peux-tu me montrer un projecteur dont la norme triple est plus grande que 2 ?
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 25 Oct 2012, 00:50
par Supernova » 25 Oct 2012, 00:50
Doraki a écrit:Peux-tu me montrer un projecteur dont la norme triple est plus grande que 2 ?
SOIT E un evn de dim n, soit B=(e1, ... ,en) une base de E
on munit E par la norme infinie ( pour tou x = x1 e1 + .... + xn en dans E, ||x||=max |xi| 1 2
c'est ça ce que tu veux?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Oct 2012, 00:51
par Doraki » 25 Oct 2012, 00:51
Ouais. Et donc tu peux fabriquer une suite qui n'a pas de valeur d'adhérence dans les projecteurs ?
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 25 Oct 2012, 21:16
par Supernova » 25 Oct 2012, 21:16
Doraki a écrit:Ouais. Et donc tu peux fabriquer une suite qui n'a pas de valeur d'adhérence dans les projecteurs ?
Exact. on procèdera de la même façon pour prouver que cet ensemble n'est pas borné :lol3:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Oct 2012, 21:25
par Doraki » 25 Oct 2012, 21:25
En dimension finie un fermé est compact si et seulement si il est borné, donc j'me prends la tête un peu pour rien ouais.
-
Supernova
- Membre Relatif
- Messages: 224
- Enregistré le: 19 Déc 2011, 23:33
-
 par Supernova » 25 Oct 2012, 21:29
par Supernova » 25 Oct 2012, 21:29
Il y a plein de prop qui facilitent la tâche en dimension finie, heureusement ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
est une suie de projecteurs qui converge vers u dans L(E,E) alors u est un projecteur
car
est un projecteur
