Etablir relation de recurrence avec intégration

[mokmap]

bonjour,
pour mes révision, je faisait un exercice, et je suis totalement bloquer des la premiére questions.

la question est :

On pose In(x) = intégral (dx/(x²+1)^n) avec n appartenent à [1; +00 [

1/ Etablir la relation de récurrence: 2n*In+1(x) = x/(x²+1)^n + (2n - 1 )In(x)


en intégrent In(x) j'arrive à

In(x) = x/(x² + 1 )^n + 2n intégral[ x²/(x² + 1)^(n+1) dx ]

en choisie pour u= 1/(x²+1)^n => du = - 2nx/(x²+1)^(n+1)

et v= x <= dv = dx


mais aprés je ne sais pas quoi faire , est-ce que quelqu'un a une idée ?


merci

[Ben314]

Bonsoir,
Je ne comprend pas trop tes notations : quand tu écrit "intégral(...)", c'est l'intégrale de où à où ? De plus, je ne vois pas où intervient le 'x' de In(x) dans ta formule et s'il intervient dans les bornes de l'intégrale, tu devrait appeler 't' le paramètre d'intégration pour ne pas t'embrouiller.

Modulo ces incompréhentions, l'intégralle est "classique" : tu fait une intégration par parties en prenant et 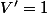puis tu écrit que

EDIT : visiblement, c'est bien le début de ce que tu as fait : il te manque seulement "l'astuce"

[mokmap]

quand j'écrit intégral ( .... ) c'est parce que je ne sais pas comment mettre le signe d'intégrale, si non l'intégral comment de la 1ére parenthése à la derniére .

et pour ce qui est des bornes, il n'y en as pas, ici on travail sans bornes.

pour le DT ben sa ne vas pas parce qu'on intégre en fonction de x et sa ne m'embrouille pas ne vous inquiété pas pour sa ( c'est vrai que écrit sans les signe mathématique c'est difficiles de comprendre je scaneré les équition pour les mettre en image sa serais plus comprehensible.

et quand j'écrit In(x) c'est I indice n de x.


pour finir est-ce que tu peut détailler ton explication j'ai aps trés bien comprie.

merci

[Ben314]

Pour ce qui est du In(x) et du reste, j'avais compris. Le fait que tu n'utilise pas LaTeX rend les choses plus difficilement lisible, mais c'était pas ça mon problème : c'était les bornes de l'intégrale :

... pour ce qui est des bornes, il n'y en as pas, ici on travail sans bornes...

Cela ne me satisfait que trés moyennement, la notation "d'intégrale sans borne" signifie en général que l'on cherche des primitives et je n'aime pas du tout cette notation car il y a plusieurs primitives à une même fonction d'où de grosses possibilitées d'erreurs, en particulier si on fait des changement de variables...
En résumé, je te conseillerais quand même d'écrire plutôt que pour le cas ou un jour tu doive faire des changement de variables....

En ce qui concerne l'indic. je te suggérais d'écrire

Ce qui te permet d'écrire en fonction de et de .
Il te suffit alors de faire passer tout les à gauche du = pour avoir le résultat demandé.

[mokmap]

ok merci pour tout, je vais regarder si j'y arrive avec tes 2 methodes ( changement de variable et donc intégration avec bornes et avec l'égalité )
et on verra si j'y arrive.

en tout cas mercie beaucoup.



ps : tu les fais comment les signe intégrale, mettre n+1 en puissance .... ?