Etablir une bijection

[Marquis91]

Voici la fonction
FONCTION

Je dois montrer que phi établit une bijection entre les entiers relatifs et Z. Merci pour vos aides.

[SaintAmand]

Je dois montrer que phi établit une bijection entre les entiers relatifs et Z.

est mal définie.

[Luc]

Voici la fonction
FONCTION

Je dois montrer que phi établit une bijection entre les entiers relatifs et Z. Merci pour vos aides.

Euh...
Z c'est l'ensemble des entiers relatifs... Tu veux vraiment construire une bijection de Z dans Z? L'identité convient...

[Marquis91]

Euh...
Z c'est l'ensemble des entiers relatifs... Tu veux vraiment construire une bijection de Z dans Z? L'identité convient...

Oui c'est ce que je dois faire. Comment puis-je appliquer l'identité ?

[Luc]

Oui c'est ce que je dois faire. Comment puis-je appliquer l'identité ?

Est-ce que tu comprends ce que tu fais?
Montrer qu'il existe une bijection d'un ensemble dans lui même n'a aucun intérêt puisque la fonction qui à x associe x est évidemment bijective.

[Marquis91]

Est-ce que tu comprends ce que tu fais?
Montrer qu'il existe une bijection d'un ensemble dans lui même n'a aucun intérêt puisque la fonction qui à x associe x est évidemment bijective.

J'ai mal préciser l'énoncé désolé. On a deux Z différents, celui des entiers relatif et un ensemble Z.
Les indications de Z ce trouve sur cette image :
http://imageshack.us/a/img259/7982/daumequation13477854813.png

[Kikoo <3 Bieber]

Je crois que ton Z c'est

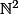
Euh non, je dis de la merde :stupid_in

[Marquis91]

Je pense qu'il y a une part de vrai dans ce que tu dis mais pas totalement. Je pense que ce sont les éléments de Z qui appartiennent à \mathbb{N}^2 . Mais je ne suis pas sur qu'on puissent dire que Z est \mathbb{N}^2

[Luc]

Je pense qu'il y a une part de vrai dans ce que tu dis mais pas totalement. Je pense que ce sont les éléments de Z qui appartiennent à \mathbb{N}^2 . Mais je ne suis pas sur qu'on puissent dire que Z est \mathbb{N}^2

Ok, tout s’éclaire.
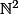
En fait ton Z ce n'est pas , c'est simplement deux copies de réunies. Je ne comprends d'ailleurs pas pourquoi on a pas plutôt choisit . Mais en gros l’idée est qu'a un nombre relatif positif tu fais correspondre sa copie dans N1, a un nombre relatif négatif tu fais correspondre sa copie dans N2, et a 0 tu fais correspondre (0,0). Tu peux vérifier que cette correspondance est bijective.

[Marquis91]

Comment je fais pour vérifier la bijection de cette correspondance ?

[Luc]

Comment je fais pour vérifier la bijection de cette correspondance ?

Déjà tu commences par la définir rigoureusement. Ensuite ça sera assez facile.

[Marquis91]

Ok merci de ton aide.