Bonjour
Je souhaiterais avoir votre avis sur la rédaction que je fais dans cet exercice. Est elle correcte et rigoureuse ?
De plus, dans la question 1) je suis bloqué sur la réciproque
je suis parti sur une idée mais est ce la bonne ?
Merci pour votre aide
Soit E un espace vectoriel possédant une base (i ;j) formée de 2 vecteurs st soit les 2 vecteurs :
u=ai+bj et v = ci+dj avec a,b,c,d des réels.
1) Démontrer que les vecteurs u et v engendrent E ssi le déterminant D cest adire ad-bc est différent de zéro.
2) En déduire que lon à léquivalence entre les énoncés suivants :
(a) (u ;v) est une base E
(b) u et v engendrent E
(c) u et v sont indépendants
pour la question 1)
sens direct : si le déterminant est non nul
soit w un vecteur qcq de E. puisque (i ;j) est une base de E, le vecteur w sécrit comme combinaison linéaire des vecteurs i et j.
donc w = ;) i + ;) j
formons le vecteur du-bv
du-bv = (da-bc) i + (db-bd) j = (da-bc) i = D i
ainsi i = (1/D) (du-bv)
de même en formant cu+av on trouve j = (1/D) ( -cu+av)
on en déduit que tou vecteur w de E est tq :
w = ;) (1/D) (du-bv) + ;) (1/D) ( -cu+av)
soit w = (1/D) (;)d-;)c) u + (1/D) (-;)b+;)a) v
u et v étant clairement des vecteurs de E on en déduit de légalité ci dessus quils engendrent E
réciproquement :
si u et v engendrent E alors un vecteur quelconque w de E est tq w = ;) u + ;) v
soit en remplaçant w = (;)a+;)c) i + (;)b+;)d) j
prenons deux vecteurs particuliers en posant ;) = 1 et ;)=0 (on retrouve u )
puis en posant ;) = 0 et ;)=1 (on retrouve v)
le déterminant est alors D=ad-bc
mais je suis bloqué pour dire quil est non nul ???
Espace vectoriel
6 messages
- Page 1 sur 1
La démonstration directe est bonne.
Tu peux faire comme ceci pour la réciproque :
Supposons que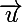 et
et 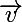 engendrent E. Alors quel que soit
engendrent E. Alors quel que soit 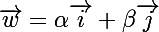 on peut trouver
on peut trouver 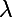 et
et 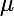 tels que :
tels que :
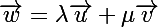
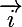 et
et 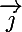 engendrent E donc il existe
engendrent E donc il existe 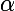 et
et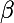 tels que :
tels que :
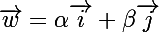
Donc quels que soient les réels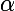 et
et 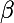 , il existe
, il existe 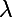 et
et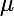 tels que :
tels que :
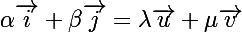
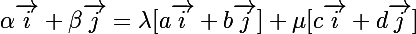
 \vec{i}+(\lambda b + \mu d) \vec{j}])
Cela est équivalent à :
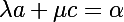
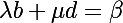
Pour que quels que soient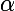 et
et 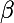 , il existe
, il existe 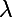 et
et 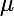 vérifiant ces équations, il faut et il suffit que le déterminant (ad-bd) soit non nul.
vérifiant ces équations, il faut et il suffit que le déterminant (ad-bd) soit non nul.
Tu peux faire comme ceci pour la réciproque :
Supposons que
Donc quels que soient les réels
Cela est équivalent à :
Pour que quels que soient
Merci mais ce nest pas encore clair
Remarque une erreur de frappe sûrement mais D=ad-bc et non ad-bd
Je comprend bien comment tu arrives au système et en disant que le déterminant est non nul cela implique lunicité de ;) et ;)
Mais je ne vois pas en quoi le fait que D = 0 va poser problème..
On va trouver alors par exemple d =( ;)/;)) c et b =( ;)/;)) a car on peut supposer par exemple ;) non nul et ou est le pb ??
Remarque une erreur de frappe sûrement mais D=ad-bc et non ad-bd
Je comprend bien comment tu arrives au système et en disant que le déterminant est non nul cela implique lunicité de ;) et ;)
Mais je ne vois pas en quoi le fait que D = 0 va poser problème..
On va trouver alors par exemple d =( ;)/;)) c et b =( ;)/;)) a car on peut supposer par exemple ;) non nul et ou est le pb ??
steph a écrit:Remarque une erreur de frappe sûrement mais D=ad-bc et non ad-bd
Très juste !
steph a écrit:Je comprend bien comment tu arrives au système et en disant que le déterminant est non nul cela implique lunicité deet
Mais je ne vois pas en quoi le fait que D = 0 va poser problème..
On va trouver alors par exemple d =(/;)) c et b =(
/;)) a car on peut supposer par exemple
non nul et ou est le pb ??
Attends ! D'abord, il ne s'agit pas d'une équation en d et b ! d et b sont donnés. Tu n'as pas le droit d'y toucher. Il s'agit de savoir si quels que soient
2x + y = 1
4x + 2y = 1
n'a pas de solution. Et :
2x + y = 1
4x + 2y = 2
a, lui, une infinité de solutions. Le seul moyen de garantir qu'un système a toujours une solution (c'est à dire quel que soient les seconds membres donnés) est que le déterminant soit non nul ! Et dans ce cas, c'est la cerise sur le gâteau, en prime, tu as l'unicité !
ah oui c'est plus clair maintenant et
Merci pour la réponse
En fait je suis en TS et je fais ce type dexo pour le plaisir ; dans un vieux bouquin de 2nd que jai trouvé !
je voudrais quand même savoir si ce que je propose est juste et comment me sortir de mon problème en suivant ce que je voulais faire... est ce possible?. Car jai pas le corrigé
pour la question 2)
la question 1) montre l équivalence entre (b) et (c) car deux vecteurs sont indépendants ssi le déterminant dans la base B est non nul
limplication (a) vers (b) est immédiate
pour montrer que (b) implique (a) on utilise le fait que (u,v) engendre E et que lon a aussi (u,v) libre (puisque (b) équivaut à (c) )
donc système libre et générateur de E qui forme une base .
merci
Merci pour la réponse
En fait je suis en TS et je fais ce type dexo pour le plaisir ; dans un vieux bouquin de 2nd que jai trouvé !
je voudrais quand même savoir si ce que je propose est juste et comment me sortir de mon problème en suivant ce que je voulais faire... est ce possible?. Car jai pas le corrigé
pour la question 2)
la question 1) montre l équivalence entre (b) et (c) car deux vecteurs sont indépendants ssi le déterminant dans la base B est non nul
limplication (a) vers (b) est immédiate
pour montrer que (b) implique (a) on utilise le fait que (u,v) engendre E et que lon a aussi (u,v) libre (puisque (b) équivaut à (c) )
donc système libre et générateur de E qui forme une base .
merci
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
