Espace vectoriel
23 messages
- Page 2 sur 2 - 1, 2
par alavacommejetepousse » 09 Mar 2008, 15:05
soit Q dans E on cherche P dans E tel que
D(P) = Q
on écrit Q = a +b X +cX^2 a,b,c sont donc donnés
on écrit P = a' +b' X + c'X^2 a' , b',c' sont donc les inconnues
on résoud on trouve donc a',b',c' en fonction de a,b,c et on a prouvé la bijectivité de D
D(P) = Q
on écrit Q = a +b X +cX^2 a,b,c sont donc donnés
on écrit P = a' +b' X + c'X^2 a' , b',c' sont donc les inconnues
on résoud on trouve donc a',b',c' en fonction de a,b,c et on a prouvé la bijectivité de D
par Bourasland » 09 Mar 2008, 17:13
bon j'ai écrit
soit\in \mathbb{E^2})
On veut montrer que=Q)
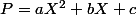
avec \in \mathbb{R^3})
avec  \in \mathbb{R^3})
On doit avoir :
Il existe donc une unique solution à ce système (si
), donc 
est bijective.
c'est ça?
soit
On veut montrer que
On doit avoir :
Il existe donc une unique solution à ce système (si
c'est ça?
23 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :