Espace vectoriel

[Bourasland]

Bonjour, on a commencé l'Algèbre avec un premier chapitre sur les espaces vectoriels et j'ai beaucoup de mal avec les exercices, pourriez vous m'aider sur cet exercice?
Voici l'énoncé (les 2 questions sont indépendantes)

1) Soit le -espace vectoriel des fonctions polynômiales définies sur , de degré inférieur ou égal à 2.
Soit . On note , définie sur .
Montrer que .
est-elle injective? surjective? Faire une discussion.

2) Soit définie sur pour .
Montrer que est une famille libre dans
Indication: regarder la dérivabilité des fonctions et raisonner par l'absurde.


- Pour la 1), je ne comprend pas du tout...
- Pour la 2), j'ai écrit:

Soit tel que:

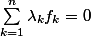
mais après je ne sais pas quoi faire et comment étudier la dérivabilité de ces fonctions...

pouvez vous m'aider pour ces deux questions?

[alavacommejetepousse]

bonsoir
1) important réflèchis encore

2) anecdotique
si tous les scalaires n'étaient pas nuls une des fonctionsf k serait combinaison des autres or fk n'est pas dérivable en xk les autres l'étant, contradictoire.

[Bourasland]

j'ai vraiment trop de mal :triste:
Pourquoi si , une des fonctions serait combinaison des autres?
et c'est quoi ?
Comment je dois étudier la dérivabilité des fonctions ?

[alavacommejetepousse]

xk = k point où fk n'est pas dérivable
si un scalaire n'est pas nul on "isole" le terme correspondant et on divise par ce scalaire

[Bourasland]

comme ça ?



et je n'est toujours pas compris le , la variable x n'a pas d'indice?, et tu veut dire ça?
?
ou ça?
?
je sais, j'ai du mal, mais il est tard... :dodo:

[alavacommejetepousse]

non j'avais noté xk au lieu de k c'est k dans l'énoncé

[Bourasland]

1) Ah OK, donc tu voulais dire que n'est pas dérivable en , c'est ça?
2) Mais pour quoi ça ne serait pas dérivable?
si , :hum:

[alavacommejetepousse]

absolument

[Bourasland]

euh, absolument pour ma question 1) ou 2)? :dodo:

et tu ne m'a pas répondu sur ce message:

"" comme ça ?

""

[Bourasland]

désolé, mais je me couche, je reprend ça demain.
Merci d'avance si tu me répond :dodo:

[alavacommejetepousse]

oui comme ça si c'est lambda n qui est non nul.

[regis183]

fk(xk)=0 et non fk=0 !!!

[Bourasland]

C'est bon pour la question 2), j'ai trouvé.
Maintenant je suis sur la question 1)... :hein:

[Bourasland]

Pour la 1), Pour montrer que c'est une application linéaire il faudrait que je montre que :

[alavacommejetepousse]

oui suffit de l écrire

[Bourasland]

pour montrer que c'est injectif, il faudrait que:

Or, ,
c'est un polynôme que si ,
Donc
est injective.
c'est bon?

[alavacommejetepousse]

oui

sauf que ker est un ensemble il manque les { }

[Bourasland]

oui oui je sais mais j'arrive pas à les faire appraitre avec LaTex ...

[Bourasland]

après pour la surjectivité de
il faudrait montrer que :
Soit
.
.
.
donc
mais je n'y arrive pas....

[alavacommejetepousse]

tu as vu le théorème du rang ?

je pense non