Espace vectoriel sur une extension d'un corps
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Jan 2010, 15:30
par Doraki » 21 Jan 2010, 15:30
C'est l'extension des scalaires ?
Ben il s'agit du produit tensoriel.
Si L est une extension de K, et V un K-ev,
On note
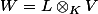
W est un L-ev, et V s'injecte dans
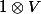
qui est un sous-K-ev de W, et qui engendre W comme L-ev.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2010, 15:49
par Ben314 » 21 Jan 2010, 15:49
Salut,
Tu peut à la rigueur le voir sans produit tensoriel en considérant une base de V, tu as V=K^I pour un certain ensemble I. Tu prend alors W=L^I et le morphisme de V dans W est évident (même coordonnées dans la base).
Dans le cas des e.v. de dim finie, ce point de vue me parrait largement suffisant, mais en dim infini, c'est pas trés malin car il faut l'axiome du choix pour exhiber une base (algébrique) et donc le produit tensoriel est bien plus adapté.
Ici, les éléments du produit sont assez facile à décrire : ce sont les couples (a,v) avec a dans L et v dans V quotientés par la relation d'équivalence (a,v)R(a',v') ssi il existe b non nul dans K tel que a'=ab et v'=b^-1v.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Jan 2010, 15:55
par Doraki » 21 Jan 2010, 15:55
J'aime pas l'image "rajouter des éléments à V", je préfère dire "changer la nature de V en rajoutant des éléments à K".
Mais oui, la construction (plutôt inintéressante) est un truc formel du genre
W est l'ensemble des sommes finies de termes de la forme
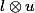
où l est dans L et u dans V, quotienté par la relation qu'il faut pour forcer à ce que :
\otimes u = l \otimes (ku) \\<br />\forall l \in L, u \in V, 0_L \otimes u = l \otimes 0_V = 0_W \\<br />\forall l_1 l_2 \in L, u \in V, (l_1 + l_2) \otimes u = l_1 \otimes u + l_2 \otimes u \\<br />\forall l \in L, u_1, u_2 \in V, l \otimes (u_1 + u_2) = l \otimes u_1 + l \otimes u_2)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2010, 16:19
par Ben314 » 21 Jan 2010, 16:19
J'ai plus ou moins dit une connerie : je croyais me rappeler que, dans ce cas, tout élément du produit tensoriel admettait un représentant de la forme (a,v) et qu'il était inutile de faire des somme, mais il me semble que c'est faux en général (i.e. pour K et L quelconque).
J'ai du confondre avec le cas "A-module => K-e.v." où K est le corps des fractions de A.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Jan 2010, 18:29
par Finrod » 21 Jan 2010, 18:29
Les représentants dont tu parles sont les générateurs.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Jan 2010, 18:43
par Ben314 » 21 Jan 2010, 18:43
Finrod a écrit:Les représentants dont tu parles sont les générateurs.
Oui, mais dans mon post #4, j'avais plus ou moins dit que tout les éléments étaient de cette forme, ce qui est faux.
Si V est de dim finie d sur K alors W est de dim d sur L mais il est de dim d.[K:L] sur K et il me semble que cela implique que les élément de W n'ont pas tous un représentant de la forme
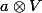
mais qu'ils sont au plus somme de [K:L] éléments de ce type.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités