EXtension de corps !

[barbu23]

Bonsoir à tous : :happy3:
Pourquoi : est une extension algebrqiue de de degré ?
Merci d'avance ! :happy3:

[Ben314]

est bien un corps qui contient le corps

Ensuite, l'élément de est algébrique sur car il est racine du polynôme (polynôme dont la variable est notée et à coefficients dans le corps )

Reste à vérifier que est irréductible sur ...

[barbu23]

Oyoyoyyy ! :doh: Je comrpends vraiment pas ce qu'il faut montrer exactement pour repondre à cette question ! tu peux m'expliquer un peu ce qui faudrait faire "Ben" ?
Merci Ben312 ! :happy3:

[barbu23]

Ce que je comprends par là est que tu as monter que : et est de degré ! ça repond pas comlètement à la question ! :happy3:

[Ben314]

Ma première réponse est NULLE ET NON AVENUE car n'est pas un corps mais seulement un anneau et ce que j'avais montré est que Q[X] est un Q[X^3] module libre de rang 3 ce qui n'est pas du tout la question (mais l'idée reste plus ou moins la bonne)...

Fait attention, l'inclusion est dans l'autre sens : un polynôme en X^3 est un polynôme en X, mais, par exemple 1+X+X^2 n'est pas un polynôme en X^3.

[barbu23]

Et pourquoi il est degré Ben ? :happy3:

[Doraki]

barbu23 tu peux me rappeler ce que c'est que le degré d'une extension de corps ?

[Ben314]

Dire que est une extention algébrique de de degrés 3 signifie que , vu comme -espace vectoriel est de dimension 3.

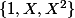
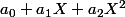
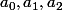
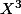
Il me parrait évident que la base doit être donc, normalement, il faudrait montrer que toute fraction rationelle en peut s'écrire, de façon unique, sous la forme où sont des fractions rationelles en , mais cela n'a rien d'évident (c'est évident pour des polynômes, mais pas pour des fractions rationelles)

Je pense donc qu'il est difficile de s'en sortir avec uniquement la définition d'extention algébrique.
Il faut donc utiliser un peu de cours...
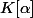
Tu as du voir qu'une extention algébrique de est de la forme où est un élément algébrique de , c'est à dire tel qu'il existe au moins un polynôme (ne pas utiliser ici qui sert déjà pour autre chose) non nul tel que .
Le plus petit (pour le degrés) polynôme unitaire t.q. est appellé le polynôme minimal de .
Il est irréductible et c'est aussi le générateur unitaire de l'idéal où ...
Le degrés de l'extention est dans ce cas le degrés du polynôme minimal .

Dans le cas présent, il est clair que le polynôme (à coeff. dans ) annule l'élément de . Reste à montrer que c'est bien lui le polynôme minimal pour prouver que l'extention est de degrés 3.
Deux voies se présentent :
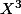
1) Montrer que est irréductible sur c'est faisable ici car, comme il est de degrés 3, s'il était factorisable, il devrait avoir une racine dans et je pense que l'on montre façilement que c'est absurde. Mais cette méthode est peu esthétique car je suis persuadé que, si à la place du 3 du il y avait 256, cela ne changerais rien (L serait un extention de degrés 256).
2) Montrer qu'aucun polynôme non nul de degrés strictement plus petit que 3 (et à coeff. dans ) n'annule . Ca je pense que c'est la bonne méthode (et en réfléchissant un peu je suis sûr que ca marche et que ca marcherait avec 256)

[yos]

il faudrait montrer que toute fraction rationelle en peut s'écrire, de façon unique, sous la forme où sont des fractions rationelles en , mais cela n'a rien d'évident (c'est évident pour des polynômes, mais pas pour des fractions rationelles)

Je pense donc qu'il est difficile de s'en sortir avec uniquement la définition d'extention algébrique

Ben non.
Si , le sous-corps de Q(X) engendré en tant qu'ev sur K par contient Q[X] et donc aussi Q(X) (car Q(X) est le plus petit sous-corps de Q(X) contenant Q[X] (corps des fractions)).

Sinon pour Barbu : une extension finie est nécessairement algébrique.

[barbu23]

MErci pour ces precisions les amis ! :happy3:

[Ben314]

Ben non.
Si , le sous-corps de Q(X) engendré en tant qu'ev sur K par contient Q[X] et donc aussi Q(X) (car Q(X) est le plus petit sous-corps de Q(X) contenant Q[X] (corps des fractions)).

Sinon pour Barbu : une extension finie est nécessairement algébrique.

Heuuuu. Yos, je comprend pas bien le "non" (il me semble que ce que j'ai écrit correspond bien à la même chose que toi...)

Peu tu m'éclairer ?

[barbu23]

Bonjour à tous : :happy3:
Soient un corps et une extension de corps de et soit .
Je voudrais savoir comment on fait en pratique pour trouver le polynome minimal de sur !
MErci de votre aide ! :happy3:

[Ben314]

Dans les exercices "pratiques" il faut dabord "sentir" un polynôme (unitaire) qui annule \alpha (c'est souvent assez évident) puis montrer que c'est le bon
1) Soit en montrant qu'il est irréductible (il y a des critères, en connait tu ?)
2) Soit en montrant qu' aucun polynôme de degré strictement plus petit ne peut annuler \alpha

Remarque : sur le plan théorique, le 1) et le 2) disent exactement la même chose, mais en pratique cela conduit des fois à des démarches différentes.

[barbu23]

Par exemple :
le polynome minimal de est ! mais je ne sais pas comment on fait pour le trouver ! :triste: :happy3:

[Ben314]

Déja, il faut préciser sur quel corps :
Si on regarde C comme une extention de C alors le polynôme minimal de i est évidement X-i
Si on regarde C comme une extention de R ce n'est surement pas X-i car ce dernier n'est pas dans R[X]. Par contre X^2+1 est bien dans R[X], il annule i et il est irréductible sur R : BINGO.

[barbu23]

Oui, c'est vrai ! merci BEn :happy3:

[Ben314]

Il y a une méthode un peu bourrin mais qui marche aussi :
Si L est un K-e.v. de dimension finie dont tu connait une base (qui, si possible n'est pas trop merdique vis à vis de la multiplication dans L)
tu considère la suite de vecteurs de L : 1 , \alpha , \alpha^2 , ...
(plus précisément, tu regarde les coordonnées de ces vecteurs dans la base). Comme L est de dimension finie, à partir d'un certain rang n, la famille (1,\alpha,\alpha^2,...,\alpha^n) est liée (tu prend évidement le n le plus petit possible) donc il existe a_0,a_1,...,a_n dans K tels que
a_0+a_1\alpha+a_2\alpha^2+...+a_n\alpha^n=0 : tu vient de trouver le polynome minimal de \alpha (en divisant par a_n car, par déf, le polynôme minimal doit être unitaire)
Arrive tu a voir pourquoi c'est bien lui ?

Un exercice d'application :
On considère l'extention de .
Déterminer le polynôme minimal de sur (indication : on pourra utiliser la base de l'espace vectoriel sur le corps )