Espace topologique

[mas_maestro]

Bonjour,
Dans la définition d'un espace topologique on dit ceci:
" Un espace topologique est un ensemble X muni d'une ensemble O de parties de X vérifiant:
1. toute intersection finie de parties de O est dans O
2. Toute réunion de parties de O est dans O
"
Ma question est de savoir pourquoi l'intersection doit etre finie mais pas la réunion.

[Arkhnor]

Salut.

On peut voir la définition des ouverts d'un espace topologique comme une tentative de généralisation des ouverts de (ou de ) à des espaces plus généraux.

Dans ces cas très simples (où la définition d'ouvert est très visuelle, et où on a une distance, par exemple la distance euclidienne, qui nous permet de définir les boules ouvertes, et par extensions les ensembles ouverts), les ouverts vérifient les propriétés qui définissent une topologie : une réunion quelconque d'ouverts est un ouvert, une intersection finie d'ouverts est un ouvert, mais il est souvent faux qu'une intersection quelconque d'ouvert soit un ouvert.

Regarde par exemple les ensembles , pour 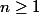. Ce sont des ouverts de , mais l'intersection de tous ces intervalles est qui n'est pas un ouvert.