Espace vectoriel topologique

[legeniedesalpages]

Bonsoir,

je bloque sur cet exercice:

Soient un e.v.t. sur , et une forme linéaire (non identiquement nulle) sur .

Montrer que si l'hyperplan est fermé, est continue.

(Montrer d'abord qu'il existe un tel que et utiliser le fait que le complémentaire de est un voisinage de ).

Bon pour commencer f est identiquement nulle, donc f est surjective (car c'est une forme linéaire), il existe alors tel que .

Ensuite on a , donc , après je ne vois pas comment montrer que est un voisinage de ,


merci pour votre aide.

[ffpower]

C est plutot que qui ne veut rien dire.On a est fermé,donc est un ouvert contenant O,c est donc un voisinage

[legeniedesalpages]

oui effectivement, une coquille de l'auteur que je n'avais pas relevé,

merci ffpower :)

[legeniedesalpages]

je ne vois pas vraiment comment en déduire la continuité, il suffit que je montre la continuité de f en O en passant par la caractérisation avec les voisinages, c'est bien ça?

[Lierre Aeripz]

Comme pour toute application linéaire, la continuité en zero équivaut à la continuité partout.

[ffpower]

que soit fermé ne signifie a priori pas que f est continue en O...

[legeniedesalpages]

que soit fermé ne signifie a priori pas que f est continue en O...

pourtant le but de l'exo c'est de montrer ça.

Je ne comprends pas l'indice de Lierre Aeripz? :marteau:

[ThSQ]

Très intéressant (et déstabilisant car on n'a "pas le droit" d'utiliser tous les trucs habituels (boules, suites, ..)) vu qu'on est dans un evt ! :marteau:

Un essai (sans garanti ...) :

Si F est fermé, il n'est pas dense (trophor) et on peut trouver un ouvert non vide U tq (*).

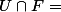
Il existe x dans E et V un voisinage de 0 tq U = x + V.

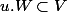
Par continuité de la multiplication par un scalaire il existe d dans K et W un voisinage de 0 tel que pour tout |u| < d.
On prend la réunion de tous ces u.W = Y de façon à obtenir un voisinage "isotrope" contenu dans Y (tq que si x est dans Y alors u.x est dans Y si |u| < 1, y'a surement un terme adéquat pour ça ...).

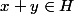
Si f(Y) n'est pas borné alors f(Y) = K par "isotropie" de Y et on peut trouver y dans Y tel que f(y) = -f(x). Mais alors contradiction avec (*).

f(Y) est donc borné ie |f(x)| < A si x dans Y, voisinage de l'origine. Maintenant c'est facile de conclure que f est continue à l'origine ! Ouf !

[ThSQ]

Ca s'appelle "balanced set" en anglais et "ensemble équilibré" en français
http://en.wikipedia.org/wiki/Balanced_set
http://fr.wikipedia.org/wiki/Espace_vectoriel_topologique