Salut,
Le 1. dit que l'application linéaire
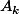
est symétrique ssi
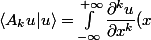\overline{u(x)}\textrm{d}x)
est réel pour toute application

. Sauf que, si tu fait de multiples intégration par partie dans
\overline{u(x)}\textrm{d}x)
, ça donne . . .
(et il va y avoir deux cas de figure selon que k est pair ou impair)P.S. Et normalement, l'usage est de dire que dans un espace
hermitien X (i.e. un e.v. sur C muni d'une forme
hermitienne définie positive), une application linéaire A:X->X telle que

pour tout u de X, c'est un
opérateur hermitien et pas un
opérateur symétrique.
Et ça tient au fait que par exemple pour des matrices nxn à coeff dans C, ben ça peut être utile dans certain contexte un peu particulier d'utiliser des
matrices symétriques (c.a.d.telle que

) et que ce n'est bien évidement pas la même chose que des
matrices hermitiennes (c.a.d.telle que

)