Espace préhilbertien non hilbertien
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par legeniedesalpages » 10 Sep 2008, 21:10
Bonsoir,
je bloque sur cette démo d'espace préhilbertien non hilbertien:
L'espace vectoriel
)
muni du produit scalaire défini par
[CENTER]
 = \Bigint_0^1 x(t)\overline{y(t)} dt)
[/CENTER]
est un espace préhilbertien complexe, pour montrer qu'il n'est pas complet, on pose:
 = \inf(n,t^{-\frac{1}{3}}))
. On a
[CENTER]
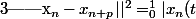 - x_{n+p}(t)|^2 dt \leq \Bigint_0^{\frac{1}{n^3}} t^{-\frac{2}{3}} dt)
[/CENTER]
C'est la dernière égalité qui me gêne, pour la montrer j'ai essayé en écrivant
en termes d'indicatrice:
 = t^{-\frac{1}{3}} \mathbb{1}_{[0,\frac{1}{n^3}[}(t)+n\mathbb{1}_{[\frac{1}{n^3},1]}(t))
,
j'obtiens
-x_{n+p}(t)| = |t^{-\frac{1}{3}}\mathbb{1}_{[\frac{1}{(n+p)^3},\frac{1}{n^3}[}(t) -n\mathbb{1}_{[\frac{1}{(n+p)^3},\frac{1}{n^3}[}(t) - p\mathbb{1}_{[ \frac{1}{(n+p)^3},1]}(t)| =\\ |(t^{-\frac{1}{3}}-n)\mathbb{1}_{[\frac{1}{(n+p)^3},\frac{1}{n^3}[}(t) - p\mathbb{1}_{[ \frac{1}{(n+p)^3},1]}(t)|)
mais je ne vois pas comment aller plus loin :marteau:
Merci pour votre aide.
-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
par nuage » 10 Sep 2008, 21:20
Salut,
si
alors
-x_{n+p}(t)=t^{-1/3}-t^{-1/3}=0)
Sinon on a
-x_{n+p}(t)|<t^{-1/3}-n)
ce qui permet de conclure.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 10 Sep 2008, 21:25
tu peux comparer
et
sur [n^-3 ; 1] ?
Ensuite c'est juste une majoration très grossière de
 - x_{n+p}(t)|^2)
par t^(-2/3)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
