Espace de hilbert et espace fermé

[muse]

Bonjour tout le monde.

Voila dans mon cours j'ai marqué:

Vh est un s.e.v de dimension finie de V donc c'est un fermé. Ici V est un espace de dimension infinie et c'est un Hilbert.

Je ne comprends pas pourquoi Vh est fermé.

PS: je pense pas que le fait que V soit un Hilbert soit utile.

Merci

[Nightmare]

Salut,

Tu peux voir Vh comme une intersection d'hyperplans fermés de V !

[kazeriahm]

Salut,

tu peux aussi prendre une base orthonormée de 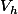(de cardinal fini donc, puisque 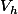est de dimension finie), et choisir une suite de 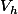convergente, notée . Pour fixé, les coordoonées de dans la base sont et on a


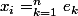
Comme converge (je note la limite), en faisant tendre vers l'infini dans l'égalité ci-dessus, on trouve que est dans 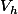, et donc que 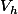est fermé

[muse]

Je comprends bien l'égalité de xi mais je ne vois pas pourquoi x serait dans Vh.

[kazeriahm]

Parce qu'à la fin on trouve


et que tous les e_k sont dans V_h

[muse]

Ok génial.
Merci beaucoup :)