Equation différentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 15:37
par Frandom94 » 03 Avr 2021, 15:37
Bonjour !
Mon cours d'analyse comporte un exercice qui n'est pas corrigé et que je n'arrive pas résoudre

Pourriez-vous y jeter un coup d'œil ?
On considère l'équation différentielle
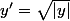
.
1) Déterminer la fonction f dans l'écriture de la forme y'= f(t,y).
2) Montrer que les hypothèses du théorème de Cauchy-Lipschitz ne sont pas vérifiées (il faut montrer que f n'est pas localement lipschitzienne par rapport à sa deuxième variable, ce que je ne sais pas faire ).
3) Déterminer une valeur de y0 et deux solutions de l'équation définie sur R et satisfaisant y(0) = y0. Je cale aussi sur cette question.
Merci beaucoup d'avance !
Frandom94.
Modifié en dernier par
Frandom94 le 03 Avr 2021, 21:55, modifié 1 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 03 Avr 2021, 15:48
par GaBuZoMeu » 03 Avr 2021, 15:48
Bonjour,
Ta fonction f est dérivable par rapport à y en dehors de y=0. Si f était lipschitzienne de rapport k par rapport à y au voisinage de 0, que pourrais-tu dire de sa dérivée par rapport à y au voisinage de 0 ?
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 15:54
par Frandom94 » 03 Avr 2021, 15:54
Pour être sûr, f est définie par f(t,y) = racine (abs( y(t)) tout simplement ?
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 16:07
par Frandom94 » 03 Avr 2021, 16:07
On suppose que f est lipschitzienne de rapport k par rapport à y sur un voisinage de 0. Alors la dérivée de f par rapport à la variable y est bornée sur ce voisinage, ce qui est absurde car f n'est pas dérivable en 0 (taux de variation infini, si je ne me trompe pas). Absurde, d'où le résultat ! Le fait d'avoir une fonction de R X R dans R me perturbe un peu en fait...
Est-ce que tu aurais une ou deux indications pour le point 3 ?
Merci beaucoup de ton aide.

-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 03 Avr 2021, 18:16
par GaBuZoMeu » 03 Avr 2021, 18:16
Frandom94 a écrit:Pour être sûr, f est définie par f(t,y) = racine (abs( y(t)) tout simplement ?
J'écrirai plutôt
= \sqrt{|y|})
(

ne dépend pas de

).
Oublie la valeur absolue (ce qui n'est pas trop gênant si tu prends
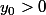
). Alors
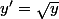
n'est pas trop dur à intégrer (c'est une équation à variables séparables). Je vois alors deux solutions avec
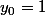
-
mathelot
 par mathelot » 03 Avr 2021, 18:32
par mathelot » 03 Avr 2021, 18:32
bonjour,
pour trouver une solution non identiquement nulle:
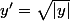
on suppose
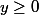
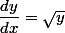
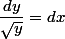 (*)
(*)on peut intégrer membre à membre.
qu'est ce que l'équation (*) donne comme solution ?
Comment en déduire une solution maximale définie sur R ?
qu'est ce qu'il se passe si y est supposée négative ?
en déduire l'existence d'au moins trois solutions maximales pour la condition initiale y0=0
Modifié en dernier par mathelot le 03 Avr 2021, 18:53, modifié 2 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 03 Avr 2021, 18:38
par GaBuZoMeu » 03 Avr 2021, 18:38
Mathelot, est-ce à toi de faire l'exercice ?
-
mathelot
 par mathelot » 03 Avr 2021, 18:51
par mathelot » 03 Avr 2021, 18:51
@GBZM: bon, j'ai tronqué mon message des deux tiers pour tenir compte de ta remarque
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 20:52
par Frandom94 » 03 Avr 2021, 20:52
mathelot a écrit:bonjour,
pour trouver une solution non identiquement nulle:
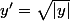
on suppose
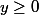
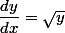
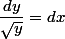 (*)
(*)on peut intégrer membre à membre.
qu'est ce que l'équation (*) donne comme solution ?
Comment en déduire une solution maximale définie sur R ?
qu'est ce qu'il se passe si y est supposée négative ?
en déduire l'existence d'au moins trois solutions maximales pour la condition initiale y0=0
Bonsoir, merci pour ta réponse. Effectivement si on suppose y>0, l'équation n'est pas dure à résoudre. On trouve y telle que
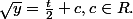
.
Mais pourquoi supposer y>0 (ou <0) ? On pourrait très bien imaginer une fonction y changeant de signe et solution de notre équation, non ?
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 21:06
par Frandom94 » 03 Avr 2021, 21:06
mathelot a écrit:bonjour,
pour trouver une solution non identiquement nulle:
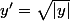
on suppose
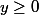
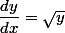
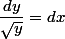 (*)
(*)on peut intégrer membre à membre.
qu'est ce que l'équation (*) donne comme solution ?
Comment en déduire une solution maximale définie sur R ?
qu'est ce qu'il se passe si y est supposée négative ?
en déduire l'existence d'au moins trois solutions maximales pour la condition initiale y0=0
Je ne vois pas comment en déduire des solutions maximales...

-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 21:09
par Frandom94 » 03 Avr 2021, 21:09
GaBuZoMeu a écrit: Frandom94 a écrit:Pour être sûr, f est définie par f(t,y) = racine (abs( y(t)) tout simplement ?
J'écrirai plutôt
= \sqrt{|y|})
(

ne dépend pas de

).
Oublie la valeur absolue (ce qui n'est pas trop gênant si tu prends
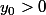
). Alors
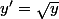
n'est pas trop dur à intégrer (c'est une équation à variables séparables). Je vois alors deux solutions avec
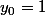
Okay, il suffit de choisir yo>0 et on a bien deux solutions pour y !
Par contre, j'ai peur de ne pas comprendre ce qui nous permet de décider y>0 (ou y<0)...
-
mathelot
 par mathelot » 03 Avr 2021, 21:44
par mathelot » 03 Avr 2021, 21:44
Frandom94 a écrit:Je ne vois pas comment en déduire des solutions maximales...

est ce que tu vois une solution triviale ? est-elle maximale ?
Le but de l'exercice, c'est de montrer que si F(t,y) n'est pas lipschitzienne en y (sauf erreur) , alors on peut perdre l'unicité de la solution du problème de Cauchy.
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 03 Avr 2021, 21:54
par Frandom94 » 03 Avr 2021, 21:54
En fait, j'ai du mal à voir ce qu'on cherche à faire... Une fois qu'on a supposé y>0, on résout l'équation à variables séparables, pas de problème... Après dire si c'est maximal ou non, je ne sais pas ;(
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 03 Avr 2021, 22:47
par GaBuZoMeu » 03 Avr 2021, 22:47
Frandom94 a écrit:On trouve y telle que
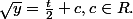
.
Ceci donne

. Ne vois-tu pas deux solutions définies sur

vérifiant
=1)
?
-
mathelot
 par mathelot » 03 Avr 2021, 22:51
par mathelot » 03 Avr 2021, 22:51
Frandom94 a écrit:En fait, j'ai du mal à voir ce qu'on cherche à faire...
on cherche au moins trois solutions au problème de Cauchy suivant:
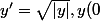=0)
Frandom94 a écrit:Une fois qu'on a supposé y>0, on résout l'équation à variables séparables, pas de problème... Après dire si c'est maximal ou non, je ne sais pas ;(
si y est supposée strictement positive, alors
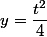
(on fait c=0)
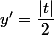
or
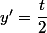
donc
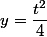
définie sur
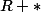
est solution.
on recolle cette solution partielle en posant

pour
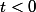
pour obtenir une solution maximale, définie sur R tout entier.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Avr 2021, 14:20
par GaBuZoMeu » 04 Avr 2021, 14:20
J'ai dit des bêtises et je t'ai embarqué sur une fausse piste : Cauchy-Lipschitz montre justement qu'il y a une seule solution au voisinage de
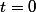
qui vérifie
=1)
, et cette solution locale se prolonge en une unique solution maximale sur

.
Tu peux voir ce que fait Mathelot.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Avr 2021, 14:50
par GaBuZoMeu » 04 Avr 2021, 14:50
Un petit dessin avec en bleu les solutions de l'équadiff :
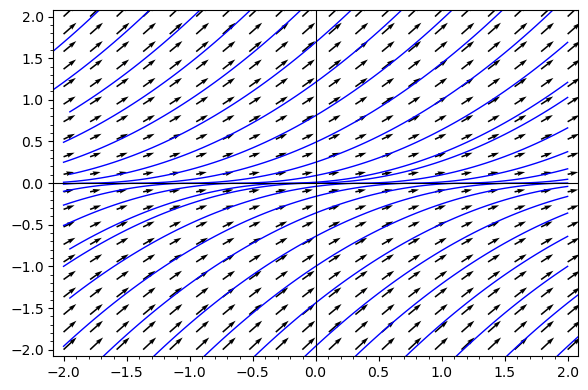
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 04 Avr 2021, 22:13
par Frandom94 » 04 Avr 2021, 22:13
Merci à vous deux pour vos réponses !
Mathelot, puis-je te demander pourquoi on a y(0)=0 ? Je ne vois pas d'où ça sort, car à priori y0 est quelconque.
Si je te suis bien, on trouve deux solutions : la solution triviale stationnaire y=0. Ensuite si y>0, on a y = t^2/4 pour t>0 . On pose ensuite y=0 sur R-* et on a une solution maximale.
Intuitivement, une solution est maximale quand elle prend place sur l'intervalle le plus grand possible, c'est bien ça ?
Merci beaucoup

-
GaBuZoMeu
- Habitué(e)
- Messages: 6148
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Avr 2021, 08:20
par GaBuZoMeu » 05 Avr 2021, 08:20
Décidément, je n'arrête pas de raconter des bêtises :
GaBuZoMeu a écrit:cette solution locale se prolonge en une unique solution maximale sur

.
Elle se prolonge, mais pas de manière unique ! La solution locale qui vérifie
=1)
s'écrit
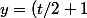^2)
et se prolonge de manière unique par cette formule sur
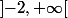
. En
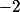
, cette solution vient tangenter l'axe des

. On peut la prolonger vers la gauche d'une infinité de façons, en suivant pendant un certain temps (éventuellement indéfiniment) l'axe des

, puis en descendant en suivant une des demi-paraboles qu'on voit dessinées ci-dessus.
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 08 Avr 2021, 12:44
par Frandom94 » 08 Avr 2021, 12:44
Merci beaucoup !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités

