Equation différentielle

[blaster]

Bonjour tout le monde,
Je viens à vous pour savoir si l'équation différentielle y'+3y=e(-3x) (condition initiale y(0)=-1) admet une solution car je n'en trouve pas. Peut-être, voir surement une erreur de ma part !
J'ai commencé par trouvé la solution de l'équation homogène :
y'+3y=0. Je trouve y1=-e(-3x).
J'essaye de trouver une solution particulière :
y2 est de la forme y2=Ae(-3x) donc y'2=-3Ae(-3x).
En remplaçant je trouve :
-3Ae(-3x)+3Ae(-3x)=e(-3x). Peu importe le A, cela donne forcément 0 et donc je ne peux trouver e(-3x) :hum:

[DamX]

Bonjour,

La méthode de variation de la constante suppose de chercher une solution sous la forme y2(x) = A(x)e(-3x), avec A une fonction de x (et non une constante), ce qui fait qu'en l'injectant dans l'équation la dérivée de A va apparaître dans l'équation, ce qui n'est pas le cas dans ce que tu as écrit..

Damien

[Ericovitchi]

Oui il y a une solution, par exemple y(x)=(x-1)e^(-3x)

la solution particulière, il fallait la chercher sous la forme Axe^(-3x) , c'était xe^(-3x) (ou faire varier la constante).

[chan79]

Bonjour tout le monde,
Je viens à vous pour savoir si l'équation différentielle y'+3y=e(-3x) (condition initiale y(0)=-1) admet une solution car je n'en trouve pas. Peut-être, voir surement une erreur de ma part !
J'ai commencé par trouvé la solution de l'équation homogène :
y'+3y=0. Je trouve y1=-e(-3x).
J'essaye de trouver une solution particulière :
y2 est de la forme y2=Ae(-3x) donc y'2=-3Ae(-3x).
En remplaçant je trouve :
-3Ae(-3x)+3Ae(-3x)=e(-3x). Peu importe le A, cela donne forcément 0 et donc je ne peux trouver e(-3x) :hum:

y2=Ae^(-3x)
y2'=A'e^(-3x)-3Ae^(-3x) et donc A'=1
y2=x*e^(-3x)

[blaster]

Merci beaucoup de votre aide rapide, je m'étais un peu égarer :we:

[deltab]

Bonjour,

Merci beaucoup de votre aide rapide, je m'étais un peu égarer :we:

L'erreur que tu as faite est dire que est la solution de l'équation différentielle homogène. La solution générale de l'équation différentielle homogène est 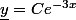, 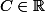(Omission d'une constante d'intégration dans le calcul) et c'est normal que tu trouves pour :