Equation differentielle

[klara]

bonjour pouvez vous m'aider svp??
MERCI
y''+ay'+by=0
(a et b 2 reels et y une fonction reelle à valeur reelle)

1)montrer que l'ensemble (s) des solutions de cette equation differentielle est un R-espace vectoriel

2)on suppose l'existence de 2 solutions y1 et y2 non nulles de (s), de conditions initiales respectives
y1(0)=yo , y'1(0)=z0 , y2(0)=v0 , y'2(0)=wo

a)montrer que la famille (y1,y2) est une famille libre de (s) si et seulement si les conditions initiales (y0,z0,v0,wo) de R verifient yowo/=z0v0.

b)montrer que si la precedente condition est verifiée ,(y1,y2) est une base de (s)

[leibniz]

Salut,
Tu te bloques où exactement?

[klara]

tout car la je suis à la fac en 1ere année de math mais l'année derniere j'ai fais un bacES donc je n'ai pas vu les equations differentielles
merci de m'aider si vous le pouvez

[Anonyme]

Tu n'as pas réelement besoin d'avoir "étudié" les équations différentielles pour résoudre les questions 1) et 2)a). Je n'en suis même pas certain pour le 2)b).
Une équation différentielle c'est simplement une équation mettant en jeu une fonction y et ses dérivées y', y'', etc...Comme par exemple : y''+ay'+by=0...

Donc pour la question 1) par exemple,

Code: Tout sélectionner

          "montrer que l'ensemble (s) des solutions de cette
          equation differentielle est un R-espace vectoriel"


il suffit de montrer que si y1 et y2 vérifient l'équation :

donc y1''+ay1'+by1=0
et y2''+ay2'+by2=0

alors, quels que soient p et q, la fonction y=p*y1+q*y2 vérifie aussi l'équation. Ca c'est pas dur.

y=p*y1+q*y2
y'=p*y1'+q*y2'
y''=p*y1''+q*y2''

et par conséquent :

y''+ay'+by = p*y1''+q*y2'' + a(p*y1'+q*y2' )+b(p*y1+q*y2 )

= p*(y1''+ay1'+by1)+q*(y2''+ay2'+by2) = 0

L'ensemble des solutions de l'équation est donc un espace vectoriel sur R !
Je n'ai pas fait la question 2)a) mais je suis quasiment certain qu'il ne s'agit que de raisonner sur les propriétés des familles libres ou pas libres, c'est-à-dire qu'il faut s'appuyer sur les propriétés des espaces vectoriels et qu'on ne fait pas réellement références aux théories des équations différentielles. Par contre, il n'est pas exclu que la question 2)b) nécessite une référence explicite à la théorie de la résolution des équations différentielles du type y''+ay'+by=0, que tu n'as pas vue...

[yos]

Bonsoir.
La question 2 est difficile telle qu'elle est posée. Sans commune mesure avec la question 1. On te demande de faire le cours en fait.
Dans le 2a, il y a un sens facile : si , la famille est libre (en effet une relation comme 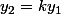entrainerait et 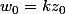, puis . La réciproque est difficile.

Le 2b est accessible. On suppose donc que est libre. Il faut montrer que si , alors n'est plus libre. On le fait en remarquant que est un élément de R² qui s'exprime dans la base de R² qu'est . On a alors qui n'est pas libre. Et donc non plus.