Equation des ondes.
41 messages
- Page 1 sur 3 - 1, 2, 3
Equation des ondes.
Bonjour,
J'ai un TD de maths auquel je n'ai pas pu assister sur l'équation des ondes, j'ai décidé de le faire par moi-même au lieu de demander la correction toute cuite pensant que ça m'aiderait pour mes examens et j'ai à peine lu l'énoncé qu'il y a quelque chose que je ne comprends pas.
http://www.noelshack.com/2022-17-4-1651 ... 232750.png
http://www.noelshack.com/2022-17-4-1651 ... 232925.png
On nous dit que la fonction est impaire donc normalement quand on utilise le théorême de Dirichlet les an sont nuls et la je vois ansinnx à la question deux alors que ça devrait être bnsinnx non ?
J'ai un TD de maths auquel je n'ai pas pu assister sur l'équation des ondes, j'ai décidé de le faire par moi-même au lieu de demander la correction toute cuite pensant que ça m'aiderait pour mes examens et j'ai à peine lu l'énoncé qu'il y a quelque chose que je ne comprends pas.
http://www.noelshack.com/2022-17-4-1651 ... 232750.png
http://www.noelshack.com/2022-17-4-1651 ... 232925.png
On nous dit que la fonction est impaire donc normalement quand on utilise le théorême de Dirichlet les an sont nuls et la je vois ansinnx à la question deux alors que ça devrait être bnsinnx non ?
Re: Equation des ondes.
Bonjour,
pour le deuxième exercice ,que vaut f(x) sur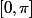
sinon vous avez (sauf erreur de ma part :
=f(x)) sur
sur 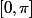
=\hat f(x)=f(x))
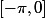
et
=\hat f(-x-2\pi)=f(x))
pour le deuxième exercice ,que vaut f(x) sur
sinon vous avez (sauf erreur de ma part :
et
Re: Equation des ondes.
Moi pour la question une j'ai ça :
https://zupimages.net/viewer.php?id=22/17/gqtn.jpg
Je ne sais pas si je dois utiliser le théorême de Dirichlet ou de Perseval puisque f(x) C0 et C1m
De toute façon, comme f(x) est impaire, je ne comprends pourquoi il y a des an dans l'expression de la série de Fourier car les an sont nuls quand f(x) impaire normalement ?
https://zupimages.net/viewer.php?id=22/17/gqtn.jpg
Je ne sais pas si je dois utiliser le théorême de Dirichlet ou de Perseval puisque f(x) C0 et C1m
De toute façon, comme f(x) est impaire, je ne comprends pourquoi il y a des an dans l'expression de la série de Fourier car les an sont nuls quand f(x) impaire normalement ?
Re: Equation des ondes.
pour moi votre fonction =|x|) est plutôt une fonction triangle
est plutôt une fonction triangle
http://www.mathematiques-lycee.com/cour ... solue.html
http://www.mathematiques-lycee.com/cour ... solue.html
Re: Equation des ondes.
ne tenez pas compte de mon message précédent,j'avais oublié que votre fonction est impair
Re: Equation des ondes.
Je suis ok avec votre graphique.
La fonction) est périodique et continue par morceaux, elle est donc développable en série de Fourier et la série convergera en tout point vers
est périodique et continue par morceaux, elle est donc développable en série de Fourier et la série convergera en tout point vers ) si
si 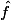 est continue en x et vers
est continue en x et vers  + \hat f(x-)}2) sinon (résultat établi par Dirichlet).
sinon (résultat établi par Dirichlet).
La fonction
Re: Equation des ondes.
autrement dit : La fonction 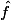 est :
est :
1)2π-périodique
2) bornée sur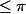
3)continue sur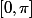
donc de classe C1 par morceaux sur R . D’après le théorème de DIRICHLET, la série de FOURIER de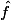 converge en tout réel x et a pour somme
converge en tout réel x et a pour somme  + \hat f(x-)}2) ( la série de Fourier de
( la série de Fourier de 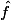 converge normalement sur R et a pour somme f)
converge normalement sur R et a pour somme f)
1)2π-périodique
2) bornée sur
3)continue sur
donc de classe C1 par morceaux sur R . D’après le théorème de DIRICHLET, la série de FOURIER de
Re: Equation des ondes.
@phylec
Pourquoi utiliser le théôreme de Dirichlet et pas celui de Perseval puisque f(x) C1m mais aussi C0m ?
Et pourquoi y a-t-il des an dans l'expression de la série puisqu'ils sont nuls quand la fonction est impaire ?
Pourquoi utiliser le théôreme de Dirichlet et pas celui de Perseval puisque f(x) C1m mais aussi C0m ?
Et pourquoi y a-t-il des an dans l'expression de la série puisqu'ils sont nuls quand la fonction est impaire ?
Re: Equation des ondes.
je ne connais pas la notation C1m,pourriez-vous me dire de quoi il s'agit.
les éléments que je vous ai fournis sont pour C1.
je crois que les an ,n'ont rien à voir avec ceux de la décomposition en série Fourier,il s'agit seulement de coefficient (le nom est mal choisi). Je suis d'accord avec vous les an de la décomposition en série de Fourier sont nuls.
les éléments que je vous ai fournis sont pour C1.
je crois que les an ,n'ont rien à voir avec ceux de la décomposition en série Fourier,il s'agit seulement de coefficient (le nom est mal choisi). Je suis d'accord avec vous les an de la décomposition en série de Fourier sont nuls.
Re: Equation des ondes.
votre question : "Pourquoi utiliser le théôreme de Dirichlet et pas celui de Perseval"
Vous ne pouvez pas utiliser Parseval, si vous n'avez pas prouvé la convergence simple(donc Dirichlet).
Vous ne pouvez pas utiliser Parseval, si vous n'avez pas prouvé la convergence simple(donc Dirichlet).
Re: Equation des ondes.
Pour votre exercice sur la corde vibrante,il faut que vous cherchiez une solution de la forme u(x,t)=f(x).g(x)
Re: Equation des ondes.
C1m veut dire dérivable par morceaux.
Ah merci @phyelec je me disais aussi c'était bizarre les an
Du coup si je récapitule le théorême de Dirichlet prouve la convergence simple et celui de Perseval la convergence normale ? Mais il ne peut pas y avoir convergence normale sans convergence simple, c'est ça ?
Ah merci @phyelec je me disais aussi c'était bizarre les an
Du coup si je récapitule le théorême de Dirichlet prouve la convergence simple et celui de Perseval la convergence normale ? Mais il ne peut pas y avoir convergence normale sans convergence simple, c'est ça ?
Re: Equation des ondes.
Alors pour la question j'ai fait ça : https://zupimages.net/viewer.php?id=22/18/alx9.jpg
Du coup je ne sais pas comment présenter les an et dire s'ils sont égaux à -1/k ou 2/(2k+1) ?
Du coup je ne sais pas comment présenter les an et dire s'ils sont égaux à -1/k ou 2/(2k+1) ?
Re: Equation des ondes.
pour votre calcul de bn,il y a une erreur :
rappel ; cos (n*0)=cos(0)=1 et non 0.
vous dites "Du coup si je récapitule le théorême de Dirichlet prouve la convergence simple et celui de Perseval la convergence normale ? Mais il ne peut pas y avoir convergence normale sans convergence simple, c'est ça ?" vous confondez pleins notions. Voici les divers type de convergence :
Convergence en norme quadratique(Parseval) :
Théorème de Parseval :f continue par morceaux, 2π-périodique ⇒ les sommes partielles (coefficients de Fourier) convergent vers f en norme quadratique (c'est dire que la formule de Parseval est vraie)
Convergence simple (Dirichlet)
f continue par morceaux, 2π-périodique (non nécessairement continue),assure la convergence ponctuelle de la série de Fourier vers la fonction f, sauf aux points de discontinuité
Convergence normale
f continue, C1 par morceaux et 2π-périodique ⇒ la série de Fourier converge normalement vers f
remarque : le "f" évoqué dans les types de convergence (ci-dessus) n'est pas le f de votre exercice,ce serait plutôt le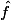
rappel ; cos (n*0)=cos(0)=1 et non 0.
vous dites "Du coup si je récapitule le théorême de Dirichlet prouve la convergence simple et celui de Perseval la convergence normale ? Mais il ne peut pas y avoir convergence normale sans convergence simple, c'est ça ?" vous confondez pleins notions. Voici les divers type de convergence :
Convergence en norme quadratique(Parseval) :
Théorème de Parseval :f continue par morceaux, 2π-périodique ⇒ les sommes partielles (coefficients de Fourier) convergent vers f en norme quadratique (c'est dire que la formule de Parseval est vraie)
Convergence simple (Dirichlet)
f continue par morceaux, 2π-périodique (non nécessairement continue),assure la convergence ponctuelle de la série de Fourier vers la fonction f, sauf aux points de discontinuité
Convergence normale
f continue, C1 par morceaux et 2π-périodique ⇒ la série de Fourier converge normalement vers f
remarque : le "f" évoqué dans les types de convergence (ci-dessus) n'est pas le f de votre exercice,ce serait plutôt le
Modifié en dernier par phyelec le 03 Mai 2022, 12:17, modifié 1 fois.
Re: Equation des ondes.
"pour votre calcul de bn,il y a une erreur :
rappel ; cos (n*0)=cos(0)=1 et non 0."
Si on multiplie un par x sur n qu'il y a devant ça fait bien zéro car x doit être remplacé par zéro
merci pour les explications sur la convergence
rappel ; cos (n*0)=cos(0)=1 et non 0."
Si on multiplie un par x sur n qu'il y a devant ça fait bien zéro car x doit être remplacé par zéro
merci pour les explications sur la convergence
Re: Equation des ondes.
"Si on multiplie un par x sur n qu'il y a devant ça fait bien zéro car x doit être remplacé par zéro": vous avez raison , j'avais relu trop vite. Sorry
Re: Equation des ondes.
Ce n'est pas grave @phyelec !
Du coup je ne sais pas comment présenter les an et dire s'ils sont égaux à -1/k ou 2/(2k+1) ?
Du coup je ne sais pas comment présenter les an et dire s'ils sont égaux à -1/k ou 2/(2k+1) ?
Re: Equation des ondes.
voici ce que je pense :
=\sum_{n=1}^{\infty} -\dfrac2n (-1)^n sin(nx))
^n)
et donc) peut s'écrire sous la forme :
peut s'écrire sous la forme :
=\sum_{n=1}^{\infty} a_n sin(nx))
pas besoin de faire la distinction entre pair et impair à ce stade de l'exo.
et donc
pas besoin de faire la distinction entre pair et impair à ce stade de l'exo.
41 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
