Equa.Diff [prépa MPSI]
15 messages
- Page 1 sur 1
Equa.Diff [prépa MPSI]
Salut,
Voilà j'ai un petit problème j'ai une équation diff à résoudre mais je n'arrive pas à trouver une primitive :
(E) (1-x)²y'=(2-x)y à résoudre sur ]-1.1[
donc j'isole y' je trouve y' = (2-x)/(1-x)² * y
La primitive de (2-x)/(1-x)² j'arrive pas a la trouver pour l'instant donc si vous pouviez m'aider à trouver cette primitive vous me serez d'un grande aide .
Mais j'ai aussi un autre problème c'est qu'après avoir résolu l'équation il me pose une autre question et alors là je pige rien
La question est : peut-on définir une solution sur un intervalle plus grand? valant 1 en 0?
Voilà j'ai un petit problème j'ai une équation diff à résoudre mais je n'arrive pas à trouver une primitive :
(E) (1-x)²y'=(2-x)y à résoudre sur ]-1.1[
donc j'isole y' je trouve y' = (2-x)/(1-x)² * y
La primitive de (2-x)/(1-x)² j'arrive pas a la trouver pour l'instant donc si vous pouviez m'aider à trouver cette primitive vous me serez d'un grande aide .
Mais j'ai aussi un autre problème c'est qu'après avoir résolu l'équation il me pose une autre question et alors là je pige rien
La question est : peut-on définir une solution sur un intervalle plus grand? valant 1 en 0?
re,
quand tu as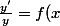)
Il faut que) ne s'annule pas sur l'intervalle considéré. Autrement dit tu peux normalement prendre l'intervalle
ne s'annule pas sur l'intervalle considéré. Autrement dit tu peux normalement prendre l'intervalle 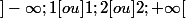 .
.
Concernant=1) il y a théorême de Cauchy qui dit qu'il faut autant de conditions que le degré de leq diff pour avoir une solution unique. Là, c'est degré 1 et tu as la condition
il y a théorême de Cauchy qui dit qu'il faut autant de conditions que le degré de leq diff pour avoir une solution unique. Là, c'est degré 1 et tu as la condition =1) .
.
Il te reste plus qu'a trouver la valeur de la constante.
quand tu as
Il faut que
Concernant
Il te reste plus qu'a trouver la valeur de la constante.
la vie est une fête 
Le problème c'est que la solution est différente selon certains intervalles.
Quand tu considères ta fonction=\frac{y'}{y}) il faut que ca soit du signe constant (parce qu'apres tu passes au log avec des valeurs absolues).
il faut que ca soit du signe constant (parce qu'apres tu passes au log avec des valeurs absolues).
(justification un peu bancale j'avoue).
D'une part tu as en supposant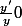 :
:=F(x)+C)
quand tu passes a lexponentielle ben yaura un probleme.
Quand tu considères ta fonction
(justification un peu bancale j'avoue).
D'une part tu as en supposant
quand tu passes a lexponentielle ben yaura un probleme.
la vie est une fête 
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
