Equa. diff. linéaire d'ordre n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2009, 12:22
par barbu23 » 26 Nov 2009, 12:22
Bonjour à tous : :happy3:
Je voudrai résoudre l'équation differentiele suivante, mais je ne vois pas comment proceder :
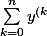} = 0 $)
Merci de votre aide ! :happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 12:24
par girdav » 26 Nov 2009, 12:24
Bonjour.
Je crois que l'on peut chercher les racines du polynôme caractéristique, qui est ici
 = \bigsum_{k=0}^nx^k)
en le multipliant par exemple par
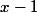
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2009, 12:27
par barbu23 » 26 Nov 2009, 12:27
Oui, les racines s'ecrivent toutes comme ça :

avec

Mais après; quelle est la solution générale ?

Les solutions forment -t-elles une base de l'espace vectoriel des solutions ?
MErci d'avance ! :happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 12:31
par girdav » 26 Nov 2009, 12:31
Il faut exclure
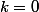
.
Sinon, en notant
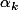
la

-ième racine

-ième, on peut regarder si la la famille
_{k\in \{1,\cdots,n\}})
est libre.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 26 Nov 2009, 12:33
par barbu23 » 26 Nov 2009, 12:33
girdav a écrit:Il faut exclure
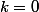
.
Sinon, en notant
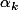
la

-ième racine

-ième, on peut regarder si la la famille
_{k\in \{1,\cdots,n-1\}})
est libre.
Ah d'accord "girdav" ! merci ! :happy3:
MErci pour la reponse que tu m'as posté sur : les-mathematiques.net
:happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 13:52
par girdav » 26 Nov 2009, 13:52
Erreur de ma part: ce sont les racines

qu'il faut considérer: la multiplication par
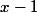
donne

.
En enlevant

on a bien

solutions.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités