Ensembles fermés, ouverts

[nico2b]

Bonjour ,

voici l'énoncé :

(a) Définissez "A est ouvert" :

(b) Définissez "A est fermé" :

(c) Définissez "A est borné" :

En utilisant les définitions précédentes, dites si les ensembles suivants sont ouverts, fermés, bornés et/ou compacts.

(a)A = ]-5,2[

Cet ensemble est ouvert et bornés...
Pour prouver borné il suffit de prendre r = 5 dans la définition ainsi B[0,5] dans représente l'ensemble [-5,5]

Pour montré qu'il est ouvert c'est là où je cale...
JE commence la preuve ainsi :

Soit x A.
Mais je n'arrive pas à trouver un r qui convient...

Auriez-vous des pistes?
Merci d'avance

[nico2b]

Personne n'as une piste pour moi? :triste:

[yos]

Bonjour.
-50 et x+5>0 on prend pour r le plus petit des réels (2-x)/2, (x+5)/2.
Fais un dessin pour comprendre ce choix.

[nico2b]

Donc si je comprends bien il faut prendre min{(2-x)/2 , (x+5)/2}?

Si c'est bien ça je ne vois pas trop pourquoi alors pcq si on prend l'exemple avec -4 A, on aura r = min (3 ; 4,5)
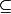
Ensuite il faudra montrer que B(4,r) A...

Mais dans les 2 cas du minimum la boule n'est pas incluse :hein: