P(N) ensemble non dénombrable.

[wotan2009]

Bonsoir,
Je dois montrer que l'ensemble des parties de N, P(N), n'est pas dénombrable.
Faut il essayer de démontrer qu'il n' y pas de bijection entre N et l'ensemble de ses parties, donc qu'on ne peut pas compter les parties de N ? Je n'arrive même pas à m'imaginer P(N), donc je vois pas comment je peux essayer de le compter. Ca ne m'étonne pas que Cantor ait perdu la raison.
Merci de l'aide.

[alavacommejetepousse]

bonsoir d une façon générale il n existe pas de surjection de E dans P(E) pour E ensemble quelconque (par l absurde en considérant A l 'ensemble des x éléments de E tels que x n 'est pas élément de f(x) où f serait une telle surjection)

[girdav]

Salut.
Pour avoir une idée intuitive du résultat, regarde quel peuvent être les éléments de . Tu prends tous les entiers naturels, et tu regarde les quels tu vas mettre dans ta partie.
Tu peux alors montrer que a la même cardinalité que . Il reste à montrer que cet ensemble n'est pas dénombrable.

[aviateur]

Bonjour
Voici une démonstration toute simple (Cantor). Soit f une fonction quelconque de vers

On désigne par E l'ensemble l'ensemble des éléments x de tels que

Mais pour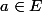 on ne peut avoir et d'autre part si 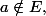f(a)=E est impossible aussi. Donc f ne peut pas être une surjection. On en déduit le résultat.

[guillaume100]

Bonsoir,
merci beaucoup je retiendrai cette astuce !