Endomorphisme symetrie

[andalous]

salut voila je dois déterminer les endomorphismes qui commutent avec toutes les symétries.J'ai pensé aux homothéties mais je n'arrive pas à la démontrer, je ne connais pas encore les matrices.
J'ai pensé partir comme ca:
soit f un endomorphisme commutant avec toutes les symétries on a alors pour tout s (symétrie) f o s=Id et en composant a droite par s comme s o s = Id on obtient f = s. Ceci valant pour toute symétrie l'endomorphisme f en question est égal à toutes les symétries? Je ne comprend pas merci de m'aider bye

[cesar]

salut voila je dois déterminer les endomorphismes qui commutent avec toutes les symétries.
soit f un endomorphisme commutant avec toutes les symétries on a alors pour tout s (symétrie) f o s=Id et en composant a droite par s comme s o s = Id on obtient f = s. Ceci valant pour toute symétrie l'endomorphisme f en question est égal à toutes les symétries? Je ne comprend pas merci de m'aider bye

comment obtenez vous f o s = Id ?
"les endomorphismes qui commutent avec toutes les symétries" : on a simplement f o s = s o f pour tout s.

[andalous]

oula oui exact je me suis un peu trop emballé mais alors comment faire je vois pas du tout

[mathelot]

bonjour,

j'ai montré que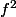 était une homothétie.

soit x tel que

1er cas) x et f(x) ont même norme.
On voit , en tracant deux vecteurs sur une feuille, qu’il y a une symétrie orthogonale qui envoie x sur f(x).
Alors il suffit de démontrer que fof(x)=x.

2ème cas :
x et f(x) n’ont pas même norme.
En choisissant un facteur multiplicatif , qui dépend de x, on se ramène au cas précedent et donc :


ensuite on en déduit que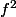 est une homothétie,
ie, le lambda ne dépend pas de x, en fait.

[yos]

Bonsoir.
fos=sof donc pour x dans Ker(s-Id), sof(x)=fos(x)=f(x) donc f(x) est aussi dans Ker(s-Id). Ainsi f laisse stable toutes les droites vectorielles . Après c'est immédiat.

J'ai pas lu tout mathelot mais il faut voir que l'intervention de la norme est pas trop dans la nature des choses.

[andalous]

ok merci a tous les deux! Yos est ce suffisant pour dire que f est une homothétie? tu as montré que si f o s = s o f alors f est une homothétie mais ne faut - il pas voir si toutes les homothéties vérifient cette condition?( la réciproque)

[yos]

Le sens "f commute avec les symétries f homothétie" est de loin le plus difficile et je n'ai pas fait la fin mais tu peux conclure avec la méthode de Mathelot dans son second cas.

La réciproque, il faut la faire bien sûr, mais elle est évidente, car les homothéties sont les endomorphismes kId.

[andalous]

j'ai essayer de reprendre ce que vous m'avez dit mais je n'arrive pas à bien rédiger puis la méthode de la norme je n'arrive pas bien a comprendre. j'ai montré que f est une homothétie si et seulement si x et f(x) sont liés donc en partant de fos=sof il faudrait que j'arrive a pour tout x dans R il existe C dans R tel que f(x) = Cx
j'ai commencé comme ca mais ca me mène a rien:

fos=sof donc fos est dans Im(s) donc dans ker(s - Id) donc so(fos)=fos=sof et en composant par s a gauche comme sos=Id il vient
fos=f=sof mais je n'en déduit rien donc c'est peut etre pas la bonne méthode merci de m'aider bye

[fahr451]

il suffit de comprendre ce qu ' a dit yos

soit x non nul dans E H un supplémentaire de la droite D engendrée par x
soit s la symétrie par rapport à D de direction H

f(s(x)) = s(f(x)) soit f(x) = s(f(x) ) donc f(x) est dans D et donc x et f(x) sont liés ; il existe lambda(x) scalaire tel que f(x) = lambda(x) x
ensuite il est facile de voir que f est une homothétie (lambda indépendant de x)

[andalous]

oui mais la s n'est pas quelconque, c'est la symétrie particuliere par rapport a D parallelement a H non?

[fahr451]

hum hum

f commute avec TOUTES les symétries en particulier celle ci

[andalous]

pas faux! merci encore ciao