égalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 24 Nov 2007, 19:33
par nada-top » 24 Nov 2007, 19:33
Bonsoir,
quelle démarche dois-je suivre pour montrer que :
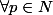
et
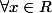
= (-1)^p\sum_{k=0}^{p}(-1)^k C_{2p+1}^k sin(2(p-k)+1)x)
merci
-
Bisounours33
- Membre Naturel
- Messages: 13
- Enregistré le: 24 Nov 2007, 18:21
-
 par Bisounours33 » 24 Nov 2007, 19:37
par Bisounours33 » 24 Nov 2007, 19:37
Je ne suis pas sûre mais moi d'instinct je partirai sur une démonstration par récurence.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Nov 2007, 19:37
par barbu23 » 24 Nov 2007, 19:37
Par récurrence !
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 24 Nov 2007, 19:39
par nada-top » 24 Nov 2007, 19:39
justement sans reccurence , dsl j'ai oublié de préciser .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2007, 19:42
par yos » 24 Nov 2007, 19:42
Formule de Moivre, formule du binôme.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Nov 2007, 19:43
par ThSQ » 24 Nov 2007, 19:43
nada-top a écrit:Bonsoir,
quelle démarche dois-je suivre pour montrer que :
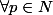
et
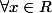
= (-1)^p\sum_{k=0}^{p}(-1)^k C_{2p+1}^k sin(2(p-k)+1)x)
merci
 = (e^{ix} - e^{-ix})/2i)
+ binome, c'est direct.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 24 Nov 2007, 19:45
par nada-top » 24 Nov 2007, 19:45
merci, je vais essayer ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités