DSE d'une intégrale

[Likoli]

Bonjour à tous !

J'ai comme le titre l'indique un DSE à faire de l'intégrale qui suit



J'aurais aimé quelques indications dans le sens où je ne vois pas comment attaquer cet exo

Merci d'avance de toute réponse !

[mathelot]

Bonjour,





l'intégrale généralisée converge plus vite qu'un arctangente , donc est parfaitement définie.

on en déduit que F(x) est une fonction analytique, développable en série de Taylor,
au voisinage de chacun de ses points , le étant obtenu en primitivant.

je ne sais pas si ça répond à la question.

ou alors tu veux un DSE au voisinage de ?

[Likoli]

Je comprends je crois.
Donc si je veux le DSE(0)
j'écris



et j'utilise par la suite le théorème d'intégration terme à terme ?

[mathelot]

bah vi, mais le rayon de convergence de la série de Mac-Laurin ne va pas couvrir tout entier

[Likoli]

Si j'ai bien compris mon prof il ne veut le DSE qu'en 0.
Néanmoins me reste une question, le moins infini ne pose-t-il pas problème dans l'intégration ?

[mathelot]

Néanmoins me reste une question, le moins infini ne pose-t-il pas problème dans l'intégration ?

si. on ne peut pas intégrer des polynômes sur un intervalle non borné. :hum:


je me demande si le problème pourrait se traiter un peu comme pour arctangente , primitive de

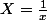
Donc commencer par poser pour se ramener à un voisinage de

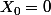
[Le_chat]

Ben... c'est quoi la dérivée de ta fonction? Tu peux parfaitement trouver un dse de la dérivée, c'est une fonction rationnelle.


Faut calculer f(0), c'est à priori un peu long mais parfaitement faisable.

[mathelot]

reste à développer


décompose la fraction en éléments simples

[Le_chat]

Ben on peut aussi dire que la dérivée de ce truc, c'est qu'on sait parfaitement développer en série entière.

[mathelot]

Ben on peut aussi dire que la dérivée de ce truc, c'est qu'on sait parfaitement développer en série entière.

avec des puissances de et formule du binome ?

[Le_chat]

Ben c'est une fraction rationnelle. On la coupe en deux fractions irréductibles sur R, de degré -2.

On connait les dse de toutes les fractions rationnelles de degré -2 à discriminant négatif, si je ne m'abuse, puis on fait la somme.

Ok, c'est extrêmement laborieux et je ne pense pas qu'on trouve à la fin un résultat super simple.

Seulement, comme trouver le dse de la bête du départ revient à trouver le dse de sa dérivée et la valeur en 0, ben je suis pas convaincu qu'on obtienne des trucs élégants autrement.