Bonjour,
C'est là que je viens de comprendre un truc énorme en mathématiques. C'est que toutes les fonctions usuelles (celles du lycée et 1ère année du supérieur) : exp, sin, cos, sh, ch, ln(1+x), 1/(1+x), homographiques, arctan, ... sont des fonctions qui sont DSE autour de 0 (ou autour d'un point quelconque, j'imagine que cela existe), donc de classe

sur un intervalle, et que pour toutes ces fonctions, leur DSE se confond avec leur DL sur l'intervalle.
Du coup pour ces fonctions, il n'y a plus rien d'étonnant à ce que leurs dérivées successives en 0 donne la fonction toute entière sur l'intervalle.
On peut en fabriquer autant qu'on veut, et même toutes. Il suffit de changer les coefficients du développement polynomial. Les polynômes ne sont que des cas particuliers de ces fonctions, à développement polynomial fini (merci Ben314).
Les fonctions exp, sin, cos, même si elles correspondent à une réalité tangible qui pré-existe à leur DSE (exp : généralisation des suites géométriques, égale à sa dérivée, cos et sin : abscisse et ordonnée d'un point qui tourne sur le cercle unité), ne sont que des cas très particuliers de ces fonctions. J'imagine qu'on peut construire de cette façon des fonctions périodiques de période autre que

, ou même qui n'ont rien à voir avec

. Ou des fonctions qui auraient d'autres propriétés étonnantes.
Du coup, je me demande si le fait qu'
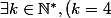, \sin^{(k)}=\sin)
et
}=\cos)
a un rapport avec le fait que ces fonctions soient périodiques. (c'est faux pour exp, qui est telle que exp'=exp, non périodique)
Bref, les fonctions DSE sont aux fonctions comme les rationnels sont aux réels : ce sont elles qu'on étudie d'abord, et qu'on étudie principalement dans le secondaire, mais il en existe plein d'autres, et c'est finalement assez trompeur, cette insistance sur les fonctions usuelles dans le secondaire. Cela me fait penser aux suites arithmétiques et géométriques : beaucoup d'élèves croient qu'il n'en existe pas d'autres (parce que c'est celles qu'on voit en tout premier quand on étudie les suites en 1ère, et ils ont du mal à le comprendre tout seuls par la suite si personne ne leur en fait la remarque) : bref, c'est un autre sujet.

