Convergence normale du DSE de -ln(1+x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 11 Avr 2012, 10:53
par Rifl3 » 11 Avr 2012, 10:53
[CENTER]

[/CENTER]
Bonjour je n'arrive pas à traiter cet exercice.
Pour la 1ère question je trouve D=]-1,1]
Mais après je n'arrive pas à démontrer la convergence normale ou uniforme, la 2)a). A chaque fois que je majore le terme général ou le reste de la série j'arrive à du |x|^n dont on ne peut rien déduire car |x| peut valoir 1, ou alors du 1/n... :/
Et je n'arrive pas non plus à démontrer qu'il n'y a pas CVN
Pourriez vous me donner une indication svp

. Merci d'avance.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Avr 2012, 11:15
par Le_chat » 11 Avr 2012, 11:15
Pour la convergence normale: on peut ici facilement revenir à la définition, une série de fonctions converge normalement ssi la somme des "normes infinies" des fonctions converge.
Sur D, quel est le sup des |fn|, si on dit que fn est la fonction que tu sommes? Conclusion?
(Par norme infinie, je désigne juste le sup des |fn|, pris pour x dans D.)
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 11 Avr 2012, 11:54
par Rifl3 » 11 Avr 2012, 11:54
Ah oui désolé --'
Dans ma tête j'avais juste l'implication que si la série des "normes infinie" converge alors la série converge normalement. Je n'ai pas pensé à la réciproque... --'
Du coup oui on obtiens la serie des 1/n qui diverge.
Mais pour la CVU?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 11 Avr 2012, 16:31
par Maxmau » 11 Avr 2012, 16:31
Rifl3 a écrit:Ah oui désolé --'
Dans ma tête j'avais juste l'implication que si la série des "normes infinie" converge alors la série converge normalement. Je n'ai pas pensé à la réciproque... --'
Du coup oui on obtiens la serie des 1/n qui diverge.
Mais pour la CVU?
Bj
Sn(x) somme partielle d'ordre n de la série
Lorsque x tend vers -1 (n fixé) Sn(x) tend vers une limite Ln
Si Sn CU vers S sur D, le critère de Cauchy (qui traduit cette CU) impliquerait que la suite (Ln) est de Cauchy
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 11 Avr 2012, 17:28
par Rifl3 » 11 Avr 2012, 17:28
Maxmau a écrit:Bj
Sn(x) somme partielle d'ordre n de la série
Lorsque x tend vers -1 (n fixé) Sn(x) tend vers une limite Ln
Si Sn CU vers S sur D, le critère de Cauchy (qui traduit cette CU) impliquerait que la suite (Ln) est de Cauchy
Ah ok, oui, c'est le "théorème d'interversion des limites" en gros.
Mais du coup une autre question me vient à l'esprit.
Si on pose D'=]-1,1[
Dans ce cas il n'y a pas non plus de CVU sur ]-1,1[?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 11 Avr 2012, 17:55
par Maxmau » 11 Avr 2012, 17:55
Oui tjs à cause du -1
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 11 Avr 2012, 18:02
par Rifl3 » 11 Avr 2012, 18:02
Maxmau a écrit:Bj
Sn(x) somme partielle d'ordre n de la série
Lorsque x tend vers -1 (n fixé) Sn(x) tend vers une limite Ln
Si Sn CU vers S sur D, le critère de Cauchy (qui traduit cette CU) impliquerait que la suite (Ln) est de Cauchy
Ah ok, oui, c'est le "théorème d'interversion des limites" en gros. Merci beaucoup

Sinon j'ai une autre petite question qui ne nécessite pas d'ouvrir un nouveau topic je pense.
Je dois trouver le rayon de convergence de la série entière de terme général

où
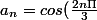)
J'ai montré que

car
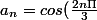1^n)
est bornée
Et j'ai montré que
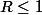
car la suite
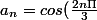1^n)
ne converge pas vers 0.
Je voulais savoir si il y avait un autre moyen pour démontrer que R<1 (inégalité, equivalent ou des choses dans le genre)
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 11 Avr 2012, 18:12
par ev85 » 11 Avr 2012, 18:12
[quote="Rifl3"]Ah ok, oui, c'est le "théorème d'interversion des limites" en gros. Merci beaucoup

Sinon j'ai une autre petite question qui ne nécessite pas d'ouvrir un nouveau topic je pense.
Je dois trouver le rayon de convergence de la série entière de terme général

où
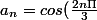)
J'ai montré que R>1 car
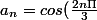1^n)
est bornée
Et j'ai montré que R1 et que R<1, c'est que tu as démontré que R n'existe pas...
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 11 Avr 2012, 18:13
par Rifl3 » 11 Avr 2012, 18:13
ev85 a écrit:Si tu as démontré que R>1 et que R<1, c'est que tu as démontré que R n'existe pas...
Fin je voulais dire que R est inférieur ou égal désolé, j'pensais qu'on me comprendrais

. Jvais changer ça.
Je ne connais pas le langage TEX il faut que j'aille voir dans un autre message quel est le code. D'ailleurs ou est référencé le langage TEX?? C'est a dire ou je peux trouver un tableau me disant que pour avoir inférieur ou égal il faut taper tel ou tel code.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 12 Avr 2012, 07:54
par Maxmau » 12 Avr 2012, 07:54
Rifl3 a écrit:Ah oui désolé --'
Dans ma tête j'avais juste l'implication que si la série des "normes infinie" converge alors la série converge normalement. Je n'ai pas pensé à la réciproque... --'
Du coup oui on obtiens la serie des 1/n qui diverge.
Mais pour la CVU?
autre suggestion pour la CVU
ici on connait S(x). on peut obtenir une expression intégrale du reste Rn(x) et montrer directement que
Rn(x) ne converge pas uniformément vers zéro / x dans ]-1,1]
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 12 Avr 2012, 09:20
par Rifl3 » 12 Avr 2012, 09:20
Maxmau a écrit:autre suggestion pour la CVU
ici on connait S(x). on peut obtenir une expression intégrale du reste Rn(x) et montrer directement que
Rn(x) ne converge pas uniformément vers zéro / x dans ]-1,1]
Je ne vois pas comment obtenir une expression intégrale de Rn(x)??
C'est à dire que Rn(x) peut être mis sous la forme d'une intégrale?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 12 Avr 2012, 09:53
par Maxmau » 12 Avr 2012, 09:53
Rifl3 a écrit:Je ne vois pas comment obtenir une expression intégrale de Rn(x)??
C'est à dire que Rn(x) peut être mis sous la forme d'une intégrale?
tu calcules:
1 - x + x² -....................+(-1)^n x^n et tu intègres
tu dois obtenir: -ln(1+x) = Sn(x) + Rn(x) avec Rn(x) sous forme intégrale
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 12 Avr 2012, 10:55
par Rifl3 » 12 Avr 2012, 10:55
Maxmau a écrit:tu calcules:
1 - x + x² -....................+(-1)^n x^n et tu intègres
tu dois obtenir: -ln(1+x) = Sn(x) + Rn(x) avec Rn(x) sous forme intégrale
aaah oui ok, c'est la formule de Taylor avec reste intégral. Pas besoin d'intégrer je pense. On l'a toute prête dans le cours ^^. Merci, je n'avais pas du tout pensé à faire comme ça, et je n'avais pas non plus fait le rapprochement entre le reste d'une fonction DSE et le reste intégral.
Et sinon pas de réponse pour le TEX??
Maxmau a écrit:Je ne connais pas le langage TEX il faut que j'aille voir dans un autre message quel est le code. D'ailleurs ou est référencé le langage TEX?? C'est a dire ou je peux trouver un tableau me disant que pour avoir inférieur ou égal il faut taper tel ou tel code.
Ou pour la série entière de cos pas d'autre méthode?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 12 Avr 2012, 11:13
par ev85 » 12 Avr 2012, 11:13
Rifl3 a écrit:Je ne connais pas le langage TEX il faut que j'aille voir dans un autre message quel est le code. D'ailleurs ou est référencé le langage TEX?? C'est a dire ou je peux trouver un tableau me disant que pour avoir inférieur ou égal il faut taper tel ou tel code.
Tu peux
regarder par ici .
Sur ce site tout ne marche pas.
\leq te donne

\geq te donne

mais rien pour \leqslant ou \geqslant.
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 12 Avr 2012, 11:54
par Rifl3 » 12 Avr 2012, 11:54
Ah ok merci beaucoup

. Et il n'y a pas quelque chose pour par exemple la somme de n=1 à n ou l'intégrale de a à b qui ne sont pas dans le formulaire???
Il y a juste les symboles

et

-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 12 Avr 2012, 12:52
par ev85 » 12 Avr 2012, 12:52
Rifl3 a écrit:Ah ok merci beaucoup

. Et il n'y a pas quelque chose pour par exemple la somme de n=1 à n ou l'intégrale de a à b qui ne sont pas dans le formulaire???
Il y a juste les symboles

et

Tu peux recopier des (bouts de) messages sur le forum et tu verras comment ils sont écrits.
\sum_{n=1}^n donne

, (
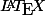
ne corrige pas les âneries mathématiques),
\int_a^b donne
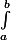
etc.
-
Rifl3
- Membre Naturel
- Messages: 59
- Enregistré le: 02 Avr 2012, 15:50
-
 par Rifl3 » 12 Avr 2012, 15:29
par Rifl3 » 12 Avr 2012, 15:29
D'accord merci beaucoup. :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités

