Bonjour à tous.
Je dois présenter la lecon "Cercles et droites dans le plan affine euclidien", leçon niveau agrégation interne.Le problème auquel je suis confronté est de présenter une leçon cohérente et ayant un "but".J imagine qu un catalogue de propriétés et définitions ne serait pas du meilleur effet.Je suis un peu pommé
A l aide .....
Droites et cercles dans le plan affine euclidien
5 messages
- Page 1 sur 1
la carpe et le lapin
bonjour,
ça n'a pas l'air évident:
d'abord un cercle et une droite ne se ressemblent pas:
les deux courbes n'ont pas le même groupe fondamental, l'une est simplement connexe , pas l'autre; l'un est compact, pas l'autre.
donc exit la topologie.
Pour leur faire jouer le même rôle, il faudrait remonter le plan sur la sphère de Riemann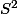 , où les droites sont des cercles passant par le pôle nord.
, où les droites sont des cercles passant par le pôle nord.
Il y avait une autre piste à explorer, celle de la dualité projective. Mais il semble que cela n'a rien à voir avec la choucroute, puisque la dualité projective échange le rôle, dans les propriétés d'incidence, entre points et droites (style thm de Céva,etc.)
Quant aux problèmes de rectfication et courbures, rien à voir non plus.
En fait, je pense que les droites et cercles ont pas grand choses à voir
(à part le fait que la droite , enroulée sur le cercle en trigonométrie est un revêtement de celui-çi). La droite est une notion affine, essentiellement
un ensemble de barycentres et le cercle une notion euclidienne, plus proche de l'ellipse.
Reste une dernière notion: l'inversion complexe qui conserve la réunion globale des deux familles . Dans cet optique, l'adjonction d'un point à l'infini
donnerait aux droites et aux cercles les mêmes propriétés topologiques.
donc, sauf erreur, l'exposé risque d'être un catalogue non structuré de propriétés sans grand lien entre elles. pour moi, ce sont deux notions (cercles et droites) qui n'ont pas grand chose à voir.
Donc pas de dualité entre eux. Et , même concernant l'aspect conique,
une conique "dégénérée" donne un couple de droites et non pas une seule droite ????
ah, si, un petit quelque chose, mais c'est maigre:
une famille de droites affines parallèles a comme orthogonal une famille de droites perpendiculaires. Et même chose , pour l'orthogonal d'un faisceau de cercles.
Le problème , sauf erreur, c'est que les notions d"'orthogonal"
ne se prolonge pas en géométrie projective.
ça n'a pas l'air évident:
d'abord un cercle et une droite ne se ressemblent pas:
les deux courbes n'ont pas le même groupe fondamental, l'une est simplement connexe , pas l'autre; l'un est compact, pas l'autre.
donc exit la topologie.
Pour leur faire jouer le même rôle, il faudrait remonter le plan sur la sphère de Riemann
Il y avait une autre piste à explorer, celle de la dualité projective. Mais il semble que cela n'a rien à voir avec la choucroute, puisque la dualité projective échange le rôle, dans les propriétés d'incidence, entre points et droites (style thm de Céva,etc.)
Quant aux problèmes de rectfication et courbures, rien à voir non plus.
En fait, je pense que les droites et cercles ont pas grand choses à voir
(à part le fait que la droite , enroulée sur le cercle en trigonométrie est un revêtement de celui-çi). La droite est une notion affine, essentiellement
un ensemble de barycentres et le cercle une notion euclidienne, plus proche de l'ellipse.
Reste une dernière notion: l'inversion complexe qui conserve la réunion globale des deux familles . Dans cet optique, l'adjonction d'un point à l'infini
donnerait aux droites et aux cercles les mêmes propriétés topologiques.
donc, sauf erreur, l'exposé risque d'être un catalogue non structuré de propriétés sans grand lien entre elles. pour moi, ce sont deux notions (cercles et droites) qui n'ont pas grand chose à voir.
Donc pas de dualité entre eux. Et , même concernant l'aspect conique,
une conique "dégénérée" donne un couple de droites et non pas une seule droite ????
ah, si, un petit quelque chose, mais c'est maigre:
une famille de droites affines parallèles a comme orthogonal une famille de droites perpendiculaires. Et même chose , pour l'orthogonal d'un faisceau de cercles.
Le problème , sauf erreur, c'est que les notions d"'orthogonal"
ne se prolonge pas en géométrie projective.
re,
bon finalement, j'ai repéré une théorie qui risque de t'intéresser:
Le bi-rapport.
Il y a le groupe des homographies ou groupe linéaire projectif de . Les transformations de ce groupe conservent les angles orientés et la famille des droites-cercles.
. Les transformations de ce groupe conservent les angles orientés et la famille des droites-cercles.
Aux homographies du plan, , on y ajoute les inversions, qui conservent aussi cercles-droites.
Les inversions ne sont pas des homographies car il y a du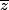 dans leur définition.
dans leur définition.
Elles (inversions+homographies) forment le groupe circulaire G. les éléments de G sont les transformations qui conservent droites-cercles.
bon finalement, j'ai repéré une théorie qui risque de t'intéresser:
Le bi-rapport.
Il y a le groupe des homographies ou groupe linéaire projectif de
Aux homographies du plan, , on y ajoute les inversions, qui conservent aussi cercles-droites.
Les inversions ne sont pas des homographies car il y a du
Elles (inversions+homographies) forment le groupe circulaire G. les éléments de G sont les transformations qui conservent droites-cercles.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
