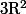Sous-groupes fermés du plan euclidien

[Nightmare]

Salut à tous :happy3:

Voici un exercice "classique" mais assez difficile lorsqu'on ne connait pas la solution. Cependant le résultat est surprenant, je vous le propose donc.

première partie : Que dire des sous-groupes fermés de ?

deuxième partie :

Notons .

a)Montrer que

défini une distance sur l'ensemble des sous-groupes fermés de
(NB personnel : Malgré sa forme barbare, cette distance semble la plus naturelle)

b) Montrer que cet ensemble est compact pour cette distance.

L'énoncé est issu d'une planche des ENS (corrigée) d'il y a 30 ans. La première question est posée sans indication (pas facile...), la deuxième admet une question intermédiaire que j'ai retirée car elle dévoilait au final toute la preuve :lol3: Cependant je la mettrais sil vous le désirez.

Bon courage :happy3:

[Nightmare]

Pas d'amateurs ?

[yos]

Les sous-groupes fermés de R² ? Comme dans R non? Les réseaux Z(a,b)+Z(c,d) (plus R² lui-même qui est fermé bien sûr). Les autres sous-groupes sont denses

[Nightmare]

Ouaip yos :happy3:

La question intéressante est celle d'après.

[yos]

La question intéressante est celle d'après.

Pfff... Bon je me sacrifie pour l'inégalité triangulaire :

.
Soit .


donc
.
Je prends le de chaque côté (croissance évidente), et j'utilise l'inclusion (presque aussi évidente) :
.
D'où :

et donc :
.
De même pour la relation symétrique (X et Z échangés).
D'où :
. Et comme c'est vrai pour tout ,
.

[Doraki]

Pour la première question.

Soit G un sousgroupe fermé de R² non trivial.
Soit x un élément non nul de G et f une forme linéaire non nulle R² -> R qui s'annule sur x. On regarde la restriction de f à G.
Alors Im(f|G) et Ker(f|G) sont des sous-groupes fermés de R (pour l'image c'est surtout parceque f(x)=0 et que R/Z est compact), donc isomorphes à {0}, Z, ou R.
Et puisque G est le produit de ces deux groupes, G est donc dans tous les cas isomorphe à l'un de ces groupes :
{0}, Z, R, Z², Z*R, R²

[yos]

{0}, Z, R, Z², Z*R, R²

J'en ai oublié quelques-uns on dirait.

[Doraki]

Pour la compacité.

Soit (Gi) une famille de sous-groupes fermés de R².
Il s'agit de montrer que cette famille a une valeur d'adhérence.

Soit X = l'ensemble des sous-groupes H fermés de R² tels qu'il existe
une suite (Gn) d'éléments de (Gi) telle que pour tout n : "H est à 1/n de Gn" : les points de H de norme 0 tel que pour presque tout i, d(X,Gi) > e.
Dans la suite (Gn) assoicée à H, ça veut dire que à partir d'un moment Gn a un point xn tel que |xn| e. La suite (xn) a une valeur d'adhérence x.
On considère H' = l'adhérence du sous-groupe engendré par H et x.
On montre que H' est dans X :
Soit n dans N, l'intersection de H' avec B(0,n) est un fermé borné de R², donc compact, et est recouvert par un nombre fini de boules B(xi,1/3n), avec
xi = hi + ki*x, hi dans H et ki dans Z.
Soit m un entier tel que |xm-x| 3n, |hi|, et |ki|*3n (pour tout i)
hi est donc à moins de 1/m < 1/3n d'un point de Gm, et tous les ki*x aussi.
Donc tout point de H' est à moins de 1/3n d'un xi, qui sont à moins de 1/3n+1/3n d'un point de Gm. Donc on a bien un Gm tel que H' est à moins de 1/n de Gm.
Et donc H' est dans X : H n'est pas maximal.

- X est un ensemble inductif :

Soit (Hk) une famille totalement ordonnée d'éléments de X, il faut trouver un majorant de (Hk) dans X.
Soit H = l'adhérence de la réunion des Hk.
On montre que H est dans X :
Soit n dans N, L'intersection de H avec B(0,n) est compact donc est recouvert par un nombre fini de B(xi,1/2n) avec xi chacun dans l'un des Hk.
Donc il existe un k tel que tous les xi sont dans Hk.
Pour ce Hk il y a un G dans la famille (Gi) tel que Hk est à moins de 1/2n de G
Alors on a bien que H est à moins de 1/n de G.
Donc H est dans X.

- X est non vide : le sous-groupe fermé {0} est dans X.

Le lemme de Zorn dit qu'alors X admet un élément maximal, qui est donc une valeur d'adhérence.
On peut en outre se servir de la question 1 pour voir que la plus grande chaîne croissante qui démarre à {0} et que l'on peut obtenir avec ces constructions est indexée par l'ordinal :

Et plutôt que d'utiliser l'axiome du choix on peut faire une étude plus explicite des chaînes de sous-groupes que l'on obtient pour montrer qu'on finit par tomber sur un maximum de X.

[Doraki]

En fait j'ai un peu l'impression d'avoir montré que l'ensemble des fermés de R² muni de cette distance est compact, et que l'ensemble des sous-groupes fermés est un fermé de cet espace topologique.

[Nightmare]

Salut Doraki :happy3:

Désolé j'avais zappé cet exercice.

J'ai lu attentivement ta preuve et à vrai dire je suis confus, je ne comprends pas ce que tu montres... (Je n'ai pas encore beaucoup travaillé sur les ensembles inductifs etc.)

[Doraki]

Tu n'as jamais utilisé le Lemme de Zorn ?

J'ai essayé de rendre ce que j'ai écrit un peu plus clair, mais bon y'a des trucs calculatoires qui sont quand même des mélanges moches de deux trucs simples, alors

2ème version :

- L'ensemble des fermés de R², muni de la distance , est un espace métrique compact.

Je fais la même preuve, avec le lemme de Zorn, sauf que cette fois ça doit être plus dur de se débarasser de l'axiome du choix vu que les chaines peuvent être beaucoup plus longues.

Soit (Fi) une famille (infinie) de fermés de R², et montrons qu'il existe un fermé qui soit une valeur d'adhérence de cette famille.

Soit X = l'ensemble des fermés F tels que pour tout il existe une infinité de fermés Fi de notre famille tels que les points de norme tel qu'il n'y a qu'un nombre fini de Fi tels que .
est compact, et
.
Donc il existe un nombre fini de , tels que .
Soir f le maximum de ces fi. Comme f est dans X, il existe une infinité de Fi tels que tout point de f de norme < est à moins de d'un point de Fi. Eh bien alors les points de norme < de F sont à moins de d'un point de ces mêmes Fi.
Donc on a bien obtenu un majorant de A dans X.

Par le lemme de Zorn, il existe un élément maximal dans A. Celui-ci est forcément une valeur d'adhérence des (Fi), et donc cela montre que l'ensemble des fermés de R² muni de la distance est compact.

- L'ensemble des sous-groupes fermés de R² est fermé.
Soit (Fn) une suite de sous-groupes fermés qui converge vers un fermé F.
Soit x et y dans F et et montrons qu'il existe z dans F tel que .
Pourvu que soit assez petit, alors :
Soit n tel que . il existe x' et y' dans Fn tels que .
Soit z' = x'+y' ; il existe z dans F tel que .
Et donc on a bien .
Et donc on a une suite de points de F qui tend vers x+y. Comme F est fermé, x+y appartient à F, et donc F est stable par +.
On montre de la même façon que 0 est dans F et que F est stable par - (sauf que c'est plus facile).
Et donc F est un sous-groupe fermé de R²,
et donc l'ensemble des sous-groupes fermés de R² est un fermé d'un espace compact, et donc il est compact.

[Nightmare]

Salut Doraki :happy3:

Désolé de répondre si tard, j'ai préféré attendre de connaitre un peu le cours de logique avant de m'attaquer à ta preuve. Quelques exercices faits sur zorn, je vais essayer de comprendre ta preuve. Je te tiens au courant !