Divisibilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 12:42
par Terras » 09 Fév 2015, 12:42
Bonjour à tous. Un petit problème de divisibilité. On considère le polynôme P(X):
=\sum_{k=0}^{p-1} 2^k X^{p-1-k})
où p est un entier strictement supérieur à 1. Soit g un entier impair.
Le problème est : existe-t-il des couples d'entiers q,c tels que :

divise
+c. g^{p})
?
J'attends vos lumières pour éclairer ma lanterne, qui reste désespérément éteinte. Merci d'avance.
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 09 Fév 2015, 14:05
par paquito » 09 Fév 2015, 14:05
Ne voyant pas de méthode évidente, j'essaie des petites valeurs de p pour voir sachant quand même que P(g) étant impair, c sera impair;
pour p=2, P(g)+cg=g(1+c)+2 et pour c=1 et g=3, P(g)+cg=8 divisible par 2^{p+0} et par 2^{p+1},
donc ce problème à des solutions et il semblerait qu'il y a des solutions pour toutes les valeurs de g, au moins avec 2^p; on a pas fait grand chose, mais cette prise de contact nous prouve qu'il y a une infinité de solutions; tentons d'aller plus loin.
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 14:35
par Terras » 09 Fév 2015, 14:35
Merci pour cette excellente remarque, quoiqu'il me semble que pour p=2, il doit y avoir un carré de g quelque part:
+c. g^{p}=g+2+ c.g^{2})
Peut-on au moins essayer de borner c et q en fonction de g et de p ?
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 09 Fév 2015, 15:40
par paquito » 09 Fév 2015, 15:40
Je suis persuadé qu'il y a des solutions pour toutes valeur de g et de p. on arrive à rien avec les congruences, donc il doit y avoir une grosse astuce pour transformer l'expression de P(X), mais je ne la vois pas. Je n'obtiens un résultat dans le cas g=1, puisque
+cg=2^p-1+c)
; d'où
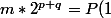+c c=m*2^{p+q}-(2^p-1))
, ce qui est toujours possible et ni c ni q ne sont bornés.
Je vais prendre un peu l'air, j'espère que ça me donnera une idée!
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 09 Fév 2015, 15:47
par paquito » 09 Fév 2015, 15:47
Terras a écrit:Merci pour cette excellente remarque, quoiqu'il me semble que pour p=2, il doit y avoir un carré de g quelque part:
+c. g^{p}=g+2+ c.g^{2})
Peut-on au moins essayer de borner c et q en fonction de g et de p ?
Bien sûr, il y a un carré!
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 16:08
par Terras » 09 Fév 2015, 16:08
paquito a écrit:Bien sûr, il y a un carré!
si p=2, c=1, g=3, comme vous l'aviez retenu, on obtient
Dans ce cas,
+c. g^{p}=3+2+3.3=14)
qui n'est pas divisible par
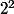
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Fév 2015, 16:18
par Doraki » 09 Fév 2015, 16:18
g^p est impair donc inversible modulo 2^(p+q), donc oui (et on peut même prendre q comme on veut)
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 16:24
par Terras » 09 Fév 2015, 16:24
Doraki a écrit:g^p est impair donc inversible modulo 2^(p+q), donc oui (et on peut même prendre q comme on veut)
Bonjour. Auriez-vous l'amabilité de développer quelque peu votre raisonnement ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Fév 2015, 17:45
par Doraki » 09 Fév 2015, 17:45
Ben on prend c = -P(g)/g^p modulo 2^(p+q)
Si t'écris g^p = 1+2u, tu peux réécrire ça en c = -P(g)*(1-2u+4u²-8u^3+...), où tu arrêtes la somme infinie dès que les termes sont des multiples de 2^(p+q)
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 18:13
par Terras » 09 Fév 2015, 18:13
Doraki a écrit:Ben on prend c = -P(g)/g^p modulo 2^(p+q)
Si t'écris g^p = 1+2u, tu peux réécrire ça en c = -P(g)*(1-2u+4u²-8u^3+...), où tu arrêtes la somme infinie dès que les termes sont des multiples de 2^(p+q)
D'accord je vois mieux, merci
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 09 Fév 2015, 21:10
par paquito » 09 Fév 2015, 21:10
Je ne suis pas du tout convaincu par l'argument de Doraki;j'ai dit que les congruences ne servaient à rien;c'est faux!Donnons nous
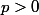
et

et

] ;pour tout k, on a

et
+cg^n= 2^p-1+c+ (2^{p+q}))
; il suffit de prendre c=m*2^{p+q}-(2^p-1)[p+q] pour avoir une solution.
Exemple:
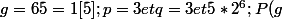=2^3-1[2^6]: cg^3=c[64])
,donc
P(g)=2^3-1[64]
et
+cg^3=2^3-1+c[64])
;il suffit donc d'avoir

désolé,je ne trouve rien de simple.
-
Terras
- Membre Naturel
- Messages: 13
- Enregistré le: 06 Jan 2015, 19:14
-
 par Terras » 09 Fév 2015, 22:04
par Terras » 09 Fév 2015, 22:04
Moi non plus je ne suis pas convaincu. Reprenons le problème, qui est : existe-il des entiers c,q tels que

divise
+c. g^{p})
?
Ce qui implique qu'il existe un entier k tel que
+c. g^{p}=k.2^{p+q})
Soit
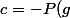/g^{p}+ k.2^{p+q}/g^{p})
. Donc la congruence de Doraki suppose que

divise k, ce que rien ne permet d'affirmer.
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 10 Fév 2015, 12:17
par BiancoAngelo » 10 Fév 2015, 12:17
Bonjour, j'ai regardé un peu...
Donc on a le polynôme
 = \sum\limits_{k=0}^{p-1} 2^kX^{p-1-k})
Soit
)
Pour
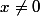
, on a :
 = \sum\limits_{k=0}^{p-1} (\frac{2}{x})^kx^{p-1})
 = x^{p-1} \sum\limits_{k=0}^{p-1} (\frac{2}{x})^k)
Pour
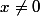
et
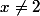
:
 = x^{p-1}\times \frac{1 - (\frac{2}{x})^p}{1 - \frac{2}{x}})
 = \frac{x^p - 2^p}{x-2})
en réduisant.
Ici, g est impair, donc ne vaut ni 0 ni 2 !
Donc pour tout g impair,
 = \frac{g^p - 2^p}{g-2})
.
Maintenant on a :
 - cg^p = \frac{g^p - 2^p + c (g-2) g^p}{g-2} = \frac{g^p(1 +cg - 2c) - 2^p}{g-2})
Or, g - 2 est impair.
Donc la question va se résumer à savoir si

divise
 - 2^p)
vu que

est pair.
Voilà, je me suis arrêté là (à vérifier si je n'ai pas écrit de sottises).
Je laisse les maîtres de la divisibilité poursuivre... :lol3:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Fév 2015, 14:52
par paquito » 10 Fév 2015, 14:52
Je suis désolé, mais hier j'avais peu de temps et j'ai écris n'importe comment;
donc tout ce que j'ai trouvé,c'est ça:
donnons nous
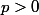
, et

et prenons

;pour tout

on a

;
d'où P(g)+cg^p \equiv 2^p-1+c [ 2^{p+q}], donc c=2^{p+q}-2^p+1 convient. ce qui fournit une infinité de solutions non triviale; de toute façon, je crois qu'il serait illusoire de les trouver toutes.
Comme je suis un maniaque de la vérification, je donne un exemple:
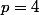
;
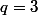
;
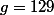
,
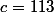
et

et

et aussi

.
Bonne continuation.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2015, 17:23
par Doraki » 10 Fév 2015, 17:23
C'est quoi votre problème avec les congruences ?
Le seul truc à savoir c'est que les inversibles mod 2^n sont les classes des entiers impairs.
Pour tout q,
2^(p+q) divise P(g) + cg^p
<=> P(g) + cg^p = 0 (mod 2^(p+q))
<=> c = -P(g)/g^p (mod 2^(p+q)) (g est impair donc est inversible et donc g^p aussi)
Donc pour toute valeur de q, les valeurs possibles de c sont les nombres qui satisfont une certaine congruence mod 2^(p+q)
Dans l'exemple de paquito, il s'agit de c = -P(129)/129^4 = -P(1)/1 = -15 = 113 (mod 128)
Donc q=3 et c = 113,241,354,... conviennent.
Si on passe à q=4 seulement la moitié de ces valeurs conviendront encore, si on passe à q=5, on en garde encore qu'une moitié et ainsi de suite.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Fév 2015, 18:17
par zygomatique » 10 Fév 2015, 18:17
BiancoAngelo a écrit:Bonjour, j'ai regardé un peu...
Donc on a le polynôme
 = \sum\limits_{k=0}^{p-1} 2^kX^{p-1-k})
Soit
)
Pour
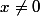
, on a :
 = \sum\limits_{k=0}^{p-1} (\frac{2}{x})^kx^{p-1})
 = x^{p-1} \sum\limits_{k=0}^{p-1} (\frac{2}{x})^k)
Pour
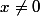
et
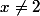
:
 = x^{p-1}\times \frac{1 - (\frac{2}{x})^p}{1 - \frac{2}{x}})
 = \frac{x^p - 2^p}{x-2})
en réduisant.
Ici, g est impair, donc ne vaut ni 0 ni 2 !
Donc pour tout g impair,
 = \frac{g^p - 2^p}{g-2})
.
Maintenant on a :
 - cg^p = \frac{g^p - 2^p + c (g-2) g^p}{g-2} = \frac{g^p(1 +cg - 2c) - 2^p}{g-2})
Or, g - 2 est impair.
Donc la question va se résumer à savoir si

divise
 - 2^p)
vu que

est pair.
Voilà, je me suis arrêté là (à vérifier si je n'ai pas écrit de sottises).
Je laisse les maîtres de la divisibilité poursuivre... :lol3:
salut
j'avais eu la même idée ... en un peu plus mieux bien .... :ptdr:
tu fais une transformation qui nécessite d'imposer
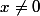
mais par contre je suis certain (de pas grand chose mais tout de même) que

(enfin dans R)
donc simplement le changement de variable j + k = p - 1 conduit à avoir
pour tout x ::
 = \sum_{k = 0}^{p - 1} \ 2^k x^{p - 1 - k} = \sum_{j = 0}^{p - 1} \ x^j 2^{p - 1 - j} = 2^{p - 1} \sum_0^{p - 1} \ \(\frac x 2 \)^k)
bien entendu je dois tout de même m'imposer x 2 pour atteindre le même résultat que toi ....
mais n'ayant rien vu de bien folichon ensuite

je n'étais pas intervenu ....
une remarque :: en calculant directement P(g) avec g impair on ne s'interdit même rien du tout ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Fév 2015, 18:31
par paquito » 10 Fév 2015, 18:31
Z/2^nZ n'est pas un corps, mais tu as raison,la classe de tout les entiers impairs est inversible mais la division des congruences n'existe pas; donc ta méthode n'est pas applicable.
Exemple:g=7, p=4, q=1: -p(g)/g^p=-477/2401=866....0,19. ça ne marche pas bien! On ne divise pas des congruences; ça merde.
Exemple: 6\equiv 1[5] et 3\equiv 3[5]....3/6\equiv3[5]!!!!! Dommage!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2015, 18:45
par Doraki » 10 Fév 2015, 18:45
quand je dis 477/2401 c'est bien évidemment 477 multiplié par l'inverse de 2401 modulo 2^(p+q)
Ca sert à quoi que je dise que 2401 est inversible modulo 2^(p+q) sinon ?
modulo 2^5, 477/2401 = 29/1 = 29.
Et mod 5 on a parfaitement 1/2 = 3/6 = 3/1 = 3 (ça ne merde pas)
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Fév 2015, 19:47
par paquito » 10 Fév 2015, 19:47
Doraki a écrit:quand je dis 477/2401 c'est bien évidemment 477 multiplié par l'inverse de 2401 modulo 2^(p+q)
Ca sert à quoi que je dise que 2401 est inversible modulo 2^(p+q) sinon ?
modulo 2^5, 477/2401 = 29/1 = 29.
Et mod 5 on a parfaitement 1/2 = 3/6 = 3/1 = 3 (ça ne merde pas)
??????????????
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Fév 2015, 19:54
par paquito » 10 Fév 2015, 19:54
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
, on a :
et
:
en réduisant.
.
divise
vu que
est pair.