Distance à un sev de dimension finie

[Arkhnor]

Bonsoir.

Je bloque sur cette question :

Soit E un espace vectoriel normé, et F un sous-espace vectoriel de E de dimension finie.
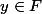
Montrer que pour tout , il existe tel que .
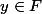
En déduire que, si , pour tout et tout , il existe tel que

C'est le "en déduire" qui me pose problème, j'ai retourné la chose dans tous les sens, je ne vois pas comment exploiter la première partie.

Si vous avez une piste, merci d'avance.

[Arkhnor]

Quelqu'un aurait une idée ?