Bonjour ,j'aimerais savoir la dimension d'une fonction de R dans R
L exo c'est qu'on a un espace vectorielle d'une fonction de R dans R auquel on applique a x->e^nx qu'on note fn.
La premiere question c'est de montrer que que f1 ... fn est une famille libre de la fonction , ça c'est simple mais la seconde on demande la dimension de la fonction de R dans R
Perso j'aurais dit 2 puisqu'elle engendre un plan mais bon comme on peut en sortir une famille a n vecteur libre c'est plutot de dimension n , ou infini si on fixe la dimension et on la depasse par n par l'absurde .
Pour le coup jsuis bloqué merci d avance pour votre aide :')
Dimension d'une fonction de R dans R
8 messages
- Page 1 sur 1
Re: Dimension d'une fonction de R dans R
Salut !
Ayant l'impression qu'il s'agit d'un exercice sur les espaces vectoriels, parler de dimension pour une fonction n'a pas de sens. Sinon, merci de préciser la définition de dimension d'une fonction parce que je ne la connais pas. Aussi serait-il peut-être mieux de nous donner l'exercice...
Ayant l'impression qu'il s'agit d'un exercice sur les espaces vectoriels, parler de dimension pour une fonction n'a pas de sens. Sinon, merci de préciser la définition de dimension d'une fonction parce que je ne la connais pas. Aussi serait-il peut-être mieux de nous donner l'exercice...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Dimension d'une fonction de R dans R
Oui en effet , l'exercice est :
On considere un R espace vectoriel de F(R,R) des fonctions définies sur R a valeurs dans R. Pour tout n appartenant a N on note fn : R->R la fonction définie par
Fn : x->e^nx
1) montre que f1 ... fn est libre
2)F(R,R) est il de dimension finie
oui c'est des fonctions autant pour moi et c'est plutot l'espace engendré
On considere un R espace vectoriel de F(R,R) des fonctions définies sur R a valeurs dans R. Pour tout n appartenant a N on note fn : R->R la fonction définie par
Fn : x->e^nx
1) montre que f1 ... fn est libre
2)F(R,R) est il de dimension finie
oui c'est des fonctions autant pour moi et c'est plutot l'espace engendré
Re: Dimension d'une fonction de R dans R
Quel que soit 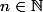 ,
,  \subset \mathcal{F}(\mathbb{R,R})) . Or que vaut
. Or que vaut ) ?
?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Dimension d'une fonction de R dans R
la dim f1...fn vaut n car on vient de montrer que c'est une famille libre ? Mais ducoup comme n appartient a N c'est un espace de dimension N ou infinie ?
Re: Dimension d'une fonction de R dans R
Notons  la dimension de l'espace vectoriel
la dimension de l'espace vectoriel ) . On vient de montrer que
. On vient de montrer que  est plus grande que n'importe quel entier naturel donc
est plus grande que n'importe quel entier naturel donc  est infinie oui !
est infinie oui !
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Dimension d'une fonction de R dans R
Hmmmmmmm d'accord merci bcp pour ton attention et je te souhaite bonne soirée !
Re: Dimension d'une fonction de R dans R
Enft je viens de comprendre mon erreur de résonnement , un espace vectoriel a une dimension fixé si je comprend bien merci encore ducoup
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
