Bonjour,
f est une fonction de

dans R, on appelle support de f l'adhérence de l'ensemble des points où f est non nulle.
On note
)
l'ensemble des fonctions f de

dans R, de classe

sur

à support compact : il existe M>0 dépendant de f avec
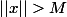
En d'autres termes :
 \subset B(0,M))
Soit A > 0 on note
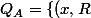 \in R^2 \times R^+ : R > ||x|| + A \})
Soit
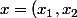)
un vecteur de

)
et
 \in Q_A)
Soit la fonction :
 = f(x_1+z_1 ,x_2+z_2))
1/ Montrer que h est à support compact. Montrer qu'il existe une boule de centre O et de rayon

qui contient son support.
2/ Montrer que l'on peut choisir
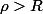
tel que la boule
)
tel que
 \subset B(O, \rho))
f est à support compact donc il existe une boule
)
avec
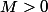
qui contient son support, f est nulle en dehors de cette boule.
Et là je bloque.
