Dimension de K[X]

par **plums** » 10 Sep 2010, 14:36

Bonsoir
question bête mais je m'interroge... quel est la dimension de K[X] ?
je sais que pour la trouver je dois trouver quel espace engendre K[X] mais je ne vois pas : pour Kn[X], j'arrive à trouver n+1 mais pour K[X] ?

Merci !

par **MacManus** » 10 Sep 2010, 14:48

Bonjour.

K[X] est ... de dimension infinie.

par **Nightmare** » 10 Sep 2010, 14:48

Salut,

Une base naturelle de K[X] est la base infinie (1,X,X²,....). K[X] est de dimension infinie (mais dénombrable) sur K.

par **girdav** » 10 Sep 2010, 14:52

Bonjour,

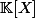
est de dimension infinie. Une base est

: cette famille est libre et génératrice (à vérifier).
Faute de frappe, merci Nightmare.

par **Nightmare** » 10 Sep 2010, 14:53

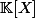
girdav a écrit:Bonjour, est de dimension infinie. Une base est .

j'aurais plutôt dit

!

par **plums** » 10 Sep 2010, 15:21

Je me disais...!

Merci bien a vous tous

par **benekire2** » 10 Sep 2010, 15:43

Salut !

En fait tu peut facilement le prouver en trouvant un isomorphisme de K[X] dans K*K[X] il me semble

par **Nightmare** » 10 Sep 2010, 21:03

où veux-tu en venir Bene?

par **benekire2** » 10 Sep 2010, 22:20

Salut,
je veut en venir au fait que K*K[X] est de dimension dim(K[X])+1 et que l'application P --> (P(0),P') montre que K[X] et K*K[X] sont isomorphe et avec l'égalité des dimensions, on arrive à une conclusion douteuse genre 1=0 :id:

par **girdav** » 11 Sep 2010, 10:14

Quelle est la loi qui fait office de produit sur

?
édit : je ne sais pas pourquoi je pensais en terme de morphisme de corps.

par **Doraki** » 11 Sep 2010, 10:19

Y'a pas de produit dans un espace vectoriel.

par **girdav** » 11 Sep 2010, 10:32

Doraki a écrit:Y'a pas de produit dans un espace vectoriel.

Mea culpa, je pensais en terme de morphisme d'anneau, ce qui n'est pas franchement logique étant donnée que l'on parle depuis le début d'espace vectoriel.

par **Nightmare** » 11 Sep 2010, 10:38

benekire2 a écrit:Salut,
je veut en venir au fait que K*K[X] est de dimension dim(K[X])+1 et que l'application P --> (P(0),P') montre que K[X] et K*K[X] sont isomorphe et avec l'égalité des dimensions, on arrive à une conclusion douteuse genre 1=0 :id:

C'est correct mais comment prouves-tu que c'est un isomorphisme? Car c'est quand même plus compliqué que d'exhiber la base canonique de K[X]...

par **benekire2** » 11 Sep 2010, 11:30

Bah son noyau est P=0 car P'=0 => P constant et P(0) assure que P=0 puis on montre que Im f = K*K[X] , c'est pas plus dur.

Cela dit c'est plus simple d'exhiber la base canonique de K[X] je te l'accorde :zen:

Dimension de K[X]

Dimension de K[X]

Qui est en ligne