Déterminant d'une matrice par blocs

[Maks]

Bonsoir !
J'ai un problème pour montrer cette assertion (qui se montre en faisant apparaître des produits bien choisis si je me souviens bien, mais je n'arrive pas à les retrouver )

Si , avec , alors .

Si quelqu'un pouvait me donner quelques indications, ça me rendrait un bon service !

Merci d'avance à tous ceux qui participeront.

[Joker62]

Haileau ;)

Faut faire la décomposition

(I;0) (A;C)
(0;B) x (0;I)

Et faire un développement par ligne pour prouver que la première à pour déterminant B et la deuxième A

[skilveg]

Salut,

Tu peux aussi le voir avec la formule qui définit le déterminant en termes de permutations: les seules permutations qui donneront une contribution non nulle dans la somme sont celles qui stabilisent la partie de gauche et celle de droite; du coup tu peux exprimer la somme comme produit de deux sommes, qui donnent les déterminants des deux blocs.

L'argument de Joker62 marche plus généralement pour des matrices par blocs quand et commutent (si je ne dis pas trop d'âneries).

J'espère que ce n'est pas trop confus...

[Maks]

Déjà, merci bien Joker, c'est ce que je cherchais ! :++:

Par contre, je n'ai pas tout compris à ta méthode, skilveg. Pourrais-tu détailler le coup des permutations, s'il te plaît ? (et sinon, pour le cas général, il faut en effet que et commutent).

Ah, et sinon, d'ailleurs, c'est quoi la décomposition pour le cas général siouplait ? :marteau:

[skilveg]

Ce que je disais c'est que si , alors , et dans la somme les seules permutations telles que pour tout sont celles qui vérifient pour (où est la taille de ) et pour . Donc elles se décomposent comme produits de permutations et . En réécrivant ce que cela veut dire pour la somme, on tombe sur le produit dont je parlais plus haut.

Dans le cas général, je ne suis pas sûr qu'on puisse dire grand chose.

[Oxypi]

Alors pour le cas général, il n'y a pas de belle formule. Cependant avec quelques hypothèses, on peut avoir des trucs sympas.

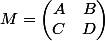
Si avec inversible, on peut utiliser la décomposition
[CENTER][/CENTER]
ce qui donne

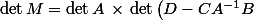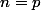
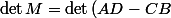Ou encore, si et et commutent, la belle formule ou une formule analogue lorsque et commutent (à savoir ).

---------------------------------------------------------------------------

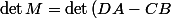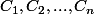
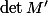
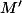
Pour le cas de la matrice triangulaire par blocs, il y a une autre (jolie) manière de raisonner. On peut considérer la forme multilinéaire alternée qui à matrices colonnes de taille associe où est la même matrice que en remplaçant par .

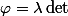
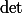
Par théorème fondamental, (l'espace vectoriel des formes -linéaires alternées sur un espace de dimension est de dimension 1) on a où est une constante et le déterminant dans la base canonique de l'espace des matrices colonnes de tailles .

Alors, en confondant -uplet de colonnes et matrice, on a (développements par rapport à la première colonne successifs) et d'où .

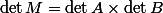
Joli, non ?

[Maks]

Merci pour toutes ces informations. J'aime en effet particulièrement le "coup" que tu utilises pour les triangulaires par bloc, en plus ça fait utiliser un théorème important :ptdr: .