Dérivée

[Akil]

Salut !
Voilà un jour que je suis bloqué sur la même question de mon DM en MPSI, je vous demande donc de l'aide.

Pour commencer, on pose : "∀x,y ∈ R*+ , g(xy) = g(x) + g(y)".

Voici la question :
"Montrer que : ∀x,y ∈ R*+, g'(xy) = g'(x)/y."

On me propose aussi un indice : "On pourra dériver, après l'avoir définie proprement et avoir justifié que c'est possible, la fonction auxiliaire h_y : x --> g(xy)."

J'arrive entre autre à démontré grâce à l'indice que "h_y'(x) = g'(x)" mais je n'arrive vraiment plus à avancer.

Merci par avance !

[GaBuZoMeu]

Bonjour,

Tu as oublié de nous dire quelles hypothèses sont faites sur .

Là, tu as dérivé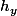 en utilisant que .
Mais si tu dérives directement en utilisant la dérivation des fonctions composées ?

[Akil]

Mais si tu dérives directement en utilisant la dérivation des fonctions composées ?

Salut GaBuZoMeu !

Sans utiliser l'indice donc ? Je vais le faire de suite pour voir si quelque chose m'apparait plus clair.

Merci pour la réponse rapide en tout cas !

[GaBuZoMeu]

Bien sûr qu'on utilise l'indice ! Ce que je te dis, c'est qu'on peut calculer la dérivée de 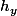de deux manières différentes.