Dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
par mathelot » 26 Déc 2019, 13:45
Tm01 a écrit:Bonjour,
Je cherche :
)')
avec :
=1/(\ln (\sqrt{x-1})))
;
Merci d'avance.
la bonne notation est
'(x))
car on dérive une fonction et pas une image.
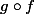
se simplifie
 (x)=\dfrac{2}{ln(x-1)})
'(x)=\dfrac{-2}{ln^2(x-1)} \times \dfrac{1}{x-1})
la dérivée de (1/u) est -u'/u^2 où u est une fonction dérivable ne s'annulant pas sur un intervalle I.
Le site Wolfram calcule les dérivées:
https://www.wolframalpha.com/input/?i=+ ... 9%7D%29%27Modifié en dernier par mathelot le 26 Déc 2019, 16:13, modifié 1 fois.
-
mathelot
par mathelot » 26 Déc 2019, 15:12
est ce que tu peux simplifier le log avant de dériver , stp ?
=\dfrac{1}{2} ln(x))
pour
-
mathelot
par mathelot » 26 Déc 2019, 15:31
Tm01 a écrit:ma prof trouve:
-1/(2(x-1)ln^2(racine(x-1)))
c'est exact mais .. non simplifié
-
mathelot
par mathelot » 26 Déc 2019, 15:40
Tu ne lis pas les réponses que je t'ai faites.
si tu ne simplifies pas le log, il faut utiliser la formule de dérivée d'une fonction composée
' = (h' \circ g \circ f) ( g' \circ f) f')
-
mathelot
par mathelot » 26 Déc 2019, 16:08
Retiens bien la maxime:
il faut simplifier avant d'effectuer
-
mathelot
par mathelot » 26 Déc 2019, 16:24
bon, pour faire comme ta prof :
'=\dfrac{-1}{ln^2(\sqrt{x-1})} \dfrac{1}{\sqrt{x-1}} \dfrac{1}{2 \sqrt{x-1}})
avec h: passage à l'inverse
g: fonction logarithme
f : racine carrée de x-1
-
mathelot
par mathelot » 26 Déc 2019, 16:38
Tm01 a écrit:ok mais elle a fait avec g rond f et pas de h ;
oui, par exemple, en associant h et g en une seule formule.
-
mathelot
par mathelot » 26 Déc 2019, 18:13
un exemple de dérivation de fonctions composées:
=\ln \left( \sin \sqrt{ \dfrac{x-1}{x+1} } \right))
on dérive d'abord le log
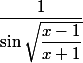
ensuite on multiplie par la dérivée du sinus:
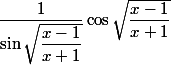
ensuite on multiplie par la dérivée de la racine:
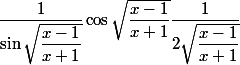
ensuite on multiplie par la dérivée de la fonction homographique:
^2})
=cotan \left( \sqrt{ \dfrac{x-1}{x+1} } \right) \dfrac{1}{\sqrt{ \dfrac{x-1}{x+1} } }\dfrac{1}{(x+1)^2})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
