Dérivée nieme de Arctan
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Mar 2008, 10:21
par zelda007 » 30 Mar 2008, 10:21
Bonjour,
Comment calculer la dérivée n-ieme de Arctan ? Je sais qu'il faut le faire par reccurence mais je ne sais pas par où commencer.
Merci
PS : Le résultat attendu est : (n  1)! cos. n. (arctan(x)) sin(n(arctan(x) +
1)! cos. n. (arctan(x)) sin(n(arctan(x) +  /2))
/2))
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 30 Mar 2008, 10:43
par Babe » 30 Mar 2008, 10:43
c'est peut etre pas la methode intelligente lol mais tu peux dérivé pour n=1,2,3,4 et voir le lien entre pour trouver la formule generale
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Mar 2008, 10:47
par zelda007 » 30 Mar 2008, 10:47
Oui je la connais mais ca m'avance pas.
J'ai vu qu'on pouvais aussi décomposer en élément simple et on obtient :
(Arctan(x))^(n) = [1/(1+x²)]^(n-1) = 1/(2i)[1/(x-i) - 1/(x+i)]^(n-1).
La dérivée n-1 ieme de : B = 1/(2i)[1/(x-i) - 1/(x+i)]^(n-1) n'est rien d'autre que :
B = 1/(2i)[(-1)^(n-1) /(x-i)^(n-1) - (-1)^(n-1) /(x+i)^(n-1)] (ce sont des puissances la)
Mais que faire après ?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 30 Mar 2008, 11:15
par ThSQ » 30 Mar 2008, 11:15
La formule a l'air fausse ... :hum:
Sinon on te donne la formule explicite il suffit de dériver et de vérifier.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Mar 2008, 11:24
par zelda007 » 30 Mar 2008, 11:24
Oui pour la reccurence, il suffit de dériver mais j'ai abandonné c'est impossible de dériver un truc pareil... Si tu as le courage, je suis preneur si tu as reussi à le faire !
 par busard_des_roseaux » 30 Mar 2008, 19:07
par busard_des_roseaux » 30 Mar 2008, 19:07
bjr,
as tu essayé :
 (1+x^2)=1)
puis la formule de Leibnitz de dérivation d'un produit à l'ordre n:
^{(n)}=\sum_{i=0}^{n} \ (_{i}^{n}) u^{(i)}v^{(n-i)})
La fonction

a peu de dérivées successives
non nulles.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 30 Mar 2008, 20:20
par zelda007 » 30 Mar 2008, 20:20
Au bois de 3 dérivées, la fonction 1 + x² est nulle mais je ne vois pas comment faire. As ton le droit de composer par les dérivées successives ? Je ne pense pas. Donc à partir de ton égalité, comment utilises tu Leibniz ?
 par busard_des_roseaux » 31 Mar 2008, 04:10
par busard_des_roseaux » 31 Mar 2008, 04:10
bjr,
Il faut chercher les exercices pour progresser !
voiçi quelques idées en vrac:
1) La formule de dérivation de Leibnitz donne une relation
entre trois dérivées successives de arctan. On peut essayer de vérifier
que les formules

proposées vérifient la même relation de récurrence
2) On peut essayer de résoudre cette équation différentielle
vérifiée par
})
en testant la solution sous forme de série entière
3)
Si
=f(x))
f est une bijection de

sur
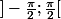
,
=g(y)=f^{-1}(y))
f et g sont des fonctions réciproques, la formule de dérivation donne
= \frac{1}{d_y \, tan(y)}=cos^2(y)=cos^2(y))
4) est-ce que la formule
=\frac{2t}{1-t^2})
avec
,x=arctan(t))
donne quelque chose ...
 par busard_des_roseaux » 31 Mar 2008, 09:28
par busard_des_roseaux » 31 Mar 2008, 09:28
re,
l'exo est intéressant. En piochant bien , il semble:
1) que l'on puisse obtenir une formule explicite de la forme
}(x)=\frac{P_n(x)}{(1+x^2)^{n+1})
sorte de formule "cartésienne"
2) qu'avec les fonctions trigo réciproques, on puisse obtenir d'autres formules
tout aussi intéressantes, en effet:
y=f(x)=arctan(x)
}=cos^2(y))
et après, on peut..redériver, en ayant ou non linéarisé le cosinus.
A chaque coup, la dérivée de fonction composée redonnera un facteur
)
 par busard_des_roseaux » 31 Mar 2008, 09:42
par busard_des_roseaux » 31 Mar 2008, 09:42
busard_des_roseaux a écrit: (1+x^2)=1) (1)
(1)
La dérivation à l'ordre n de
(1), par la formule de Leibnitz, donne la récurrence:
f^{(n+1)}(x)+2nxf^{(n)}(x)+n(n-1)f^{(n-1)}(x)=0)
en réajustant l'indice:
f^{(n+2)}(x)+2(n+1)xf^{(n+1)}(x)+n(n+1)f^{(n)}(x)=0)
Peut être peut-on maintenant utiliser cette récurrence pour obtenir une
récurrence sur les polynômes
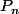
définis par:
}(x)=\frac{P_n(x)}{(1+x^2)^{n+1}})
Une fois que ça sera fait, on s'attaquera au "côté" trigonométrique.
je suis sûr que l'on va obtenir qqe chose de joli. :zen:
Très cordialement,
 par busard_des_roseaux » 31 Mar 2008, 10:01
par busard_des_roseaux » 31 Mar 2008, 10:01
zelda007 a écrit:(Arctan(x))^(n) = [1/(1+x²)]^(n-1) = 1/(2i)[1/(x-i) - 1/(x+i)]^(n-1).
ça, j'ai l'impression que ça marche aussi. :doh:
vlà ce que ça donne:
)}^{(n)}=\left( {\frac{1}{2i} ( \frac{1}{x-i}- \frac{1}{x+i}) \right) }^{(n-1)})
Les opérations "prendre la partie imaginaire" et "dériver" commutent:
)}^{(n)}={\Im \left( \frac{1}{x-i} \right)}^{(n-1)})
)}^{(n)}=\Im \left( {(\frac{1}{x-i})}^{(n-1)} \right))
)}^{(n)}={(-1)}^{n-1} (n-1)! \Im \left( \frac{1} { {(x-i)}^{n}} \right))
)}^{(n)}={(-1)}^{n-1} (n-1)! \Im \left( \frac{{(x+i)}^n} { {(x^2+1)}^{n}} \right))
)}^{(n)}={(-1)}^{n-1} \frac{(n-1)!}{{(x^2+1)}^n} \Im \left( {(x+i)}^n \right))
Ensuite , on récupère la partie imaginaire avec la formule du binôme en distinguant selon la parité de n. Il y a encore pas mal de calculs à faire. :hum:
)
=partie imaginaire de z
 par busard_des_roseaux » 31 Mar 2008, 11:41
par busard_des_roseaux » 31 Mar 2008, 11:41
Le binôme donne:
}(x) = \frac{ {(-1)}^n x (2n-1)!}{{(x^2+1)}^{2n}} \sum_{k=0}^{n-1} \, (_{2k + 1}^{2n}) {(-1)}^k x^{2k})
}(x) = \frac{ {(-1)}^n (2n)!}{{(x^2+1)}^{2n+1}} \sum_{k=0}^{n} \, (_{2k}^{2n+1}) {(-1)}^k x^{2k})
Quelqu'un peut vérifier les calculs, svp ?
maintenant, on va dériver le "côté" trigonométrique :zen:
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 31 Mar 2008, 12:22
par zelda007 » 31 Mar 2008, 12:22
busard_des_roseaux a écrit:ça, j'ai l'impression que ça marche aussi. :doh:
vlà ce que ça donne:
)}^{(n)}=\left( {\frac{1}{2i} ( \frac{1}{x-i}- \frac{1}{x+i}) \right) }^{(n-1)})
Les opérations "prendre la partie imaginaire" et "dériver" commutent:
)}^{(n)}={\Im \left( \frac{1}{x-i} \right)}^{(n-1)})
)}^{(n)}=\Im \left( {(\frac{1}{x-i})}^{(n-1)} \right))
)}^{(n)}={(-1)}^{n-1} (n-1)! \Im \left( \frac{1} { {(x-i)}^{n}} \right))
)}^{(n)}={(-1)}^{n-1} (n-1)! \Im \left( \frac{{(x+i)}^n} { {(x^2+1)}^{n}} \right))
)}^{(n)}={(-1)}^{n-1} \frac{(n-1)!}{{(x^2+1)}^n} \Im \left( {(x+i)}^n \right))
Ensuite , on récupère la partie imaginaire avec la formule du binôme en distinguant selon la parité de n. Il y a encore pas mal de calculs à faire. :hum:
)
=partie imaginaire de z
Je suis d'accords pour les calculs sauf le (n-1)! je ne vois pas d'où il sort ??
 par busard_des_roseaux » 31 Mar 2008, 12:29
par busard_des_roseaux » 31 Mar 2008, 12:29
zelda007 a écrit:Je suis d'accords pour les calculs sauf le (n-1)! je ne vois pas d'où il sort ??
Il vient des dérivées successives de
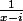
On multiplie par l'exposant négatif en dérivant.
zelda007, pourras-tu valider les calculs,in fine ?
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 31 Mar 2008, 13:35
par zelda007 » 31 Mar 2008, 13:35
Je valide jusqu'à la :
)}^{(n)}={(-1)}^{n-1} \frac{(n-1)!}{{(x^2+1)}^n} \Im \left( {(x+i)}^n \right))
Sinon pour le binôme, je pense que c'est (-1)^(2n-1) au lieu de (-1)^n pour la dérivée (2n) de Arctan.
Sinon je suis d'accord sur les calculs mais je ne vois pas ou tu veux en venir

 par busard_des_roseaux » 31 Mar 2008, 13:45
par busard_des_roseaux » 31 Mar 2008, 13:45
zelda007 a écrit:Je valide jusqu'à la :
)}^{(n)}={(-1)}^{n-1} \frac{(n-1)!}{{(x^2+1)}^n} \Im \left( {(x+i)}^n \right))
Après, pour N=2n, j'ai développé le binome selon les puissances
croissantes de

. Comme on ne s'intéresse qu'à la partie imaginaire, on somme sur les entiers de la forme 2k+1
}^k)
Une fois qu'on a la partie imaginaire, k varie de 0 à n-1,
on fait alors le changement d'indice k'=n-1-k pour obtenir des puissances croissantes de x. Evidemment, ça doit être plus simple de considérer
tout de suite des puissances croissantes de
x.
je dois y aller. :hum: Tu me diras quand tu sera assuré(e) du résultat.
 par busard_des_roseaux » 01 Avr 2008, 11:21
par busard_des_roseaux » 01 Avr 2008, 11:21
=f(x))
)
=\frac{1}{1+x^2}=cos^2(y))
Voiçi la formule trigonométrique exacte:
}(x)=(n-1)! \, (\cos(y))^n \, \sin \left( ny+n\frac{\pi}{2} \right))
il suffit de montrer :
1) que la formule est stable par dérivation par rapport à la variable x
2) qu'elle vérifie la relation de récurrence évoquée dans le fil
Zelda, je te le laisse en exercice ?
Cordialement,
 par busard_des_roseaux » 01 Avr 2008, 11:44
par busard_des_roseaux » 01 Avr 2008, 11:44
re,
à mon avis, ces formules peuvent conduire à de jolis développements
parce que:
- le développement en série de
)
utilise les
nombres de Bernoulli :zen:
- on dispose de deux formules explicites pour les dérivées nième de
)
qu'au niveau des séries (formelles), les deux développements en série
sont réciproques l'un de l'autre. Si l'on compose les deux développements en série, on doit pouvoir obtenir des relations entre les coefficients de chaque développement (

, nombres de Bernoulli, coefficients du binôme,

)
 par busard_des_roseaux » 01 Avr 2008, 12:14
par busard_des_roseaux » 01 Avr 2008, 12:14
En recopiant ce qui a été fait pour y=f(x)=arctan(x)
on peut regarder:
=\frac{1}{2} Ln \left( |\frac{1+x}{1-x} | \right))
avec
= \frac{1}{1-x^2})
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 01 Avr 2008, 16:44
par Maxmau » 01 Avr 2008, 16:44
busard_des_roseaux a écrit:=f(x))
)
=\frac{1}{1+x^2}=cos^2(y))
Voiçi la formule trigonométrique exacte:
}(x)=(n-1)! \, (\cos(y))^n \, \sin \left( ny+n\frac{\pi}{2} \right))
il suffit de montrer :
1) que la formule est stable par dérivation par rapport à la variable x
2) qu'elle vérifie la relation de récurrence évoquée dans le fil
Zelda, je te le laisse en exercice ?
Cordialement,
bonjour je n'ai pas tout suivi
une simple remarque
La formule ci- dessus ne se démontre-t-elle pas facilement par une récurrence en dérivant par rapport à y (et non par rapport à x) pour passer de n à (n+1) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
(1)
=partie imaginaire de z
}(x)=(n-1)! \, (\cos(y))^n \, \sin \left( ny+n\frac{\pi}{2} \right))