[MPSI] dérivation petit problème pour 1 question
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 10:42
par pouik » 06 Jan 2007, 10:42
Bonjour,
Il ne me reste plus qu'à répondre à la question en gras de cet exercice (je mets les autres questions car on doit surement en avoir besoin pour y répondre), mais le problème c'est que je ne vois vraiment pas comment la résoudre. Merci d'avance pour votre aide.
Soit

la fonction définie sur

par :
 = \frac{1}{\sqrt{1+x^2}})
.
1. Montrer que

est de classe

sur

et que pour tout
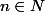
, il existe un polynôme

tel que :
}(x) = \frac{P_n(x)}{(1+x^2)^{n+\frac{1}{2}}})
Donner

, et exprimer, pour tout

en fonction de

et
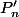
.
2. Mettre en évidence une relation simple entre les quantités
)
et
)
.
3. Etablir, pour tout
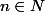
, en dérivant

fois cette égalité, la relation :
 X P_n + n^2 (1+X^2) P_{n-1} = 0)
4. Déduire de ce qui précède :
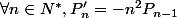
,
______________________________________________
déterminer enfin la valeur de toutes les dérivées successives de  en
en  .
.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 06 Jan 2007, 11:24
par yos » 06 Jan 2007, 11:24
=-n^2P_{n-1}(0))
et donc il est assez facile d'avoir
)
explicitement.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 11:28
par tize » 06 Jan 2007, 11:28
Bonjour,
}(0) = \frac{P_n(0)}{(1+0^2)^{n+\frac{1}{2}}}=P_n(0))
mais avec
 X P_n + n^2 (1+X^2) P_{n-1} = 0)
, on a
=-n^2P_{n-1}(0))
.
Comme
=1)
et
=0)
on en déduit que
=0)
pour tout entier n impair et ensuite, si
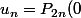)
, on a
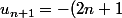^2u_n)
avec
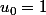
, il te reste à trouver

pour tout n...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 11:33
par pouik » 06 Jan 2007, 11:33
c'est bizarre parce que je trouve :
 = -1)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 11:34
par pouik » 06 Jan 2007, 11:34
ah non désolé en fait c'est :
 = -1)
donc ca marche.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 11:35
par pouik » 06 Jan 2007, 11:35
tize a écrit:on a
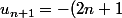^2u_n)
avec
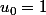
, il te reste à trouver

pour tout n...
Désolé mais je ne comprend pas la marche à suivre pour trouver

. :mur: :mur: :mur:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 13:43
par pouik » 06 Jan 2007, 13:43
pourriez vous me donner une petite piste s'il vous plait
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 15:06
par pouik » 06 Jan 2007, 15:06
faut-il faire une récurrence ou quelque-chose du genre ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 15:18
par tize » 06 Jan 2007, 15:18
=-(2n-1)^2P_{2n-2}(0)=+(2n-1)^2(2n-3)^2P_{2n-4}(0)\\<br />=-(2n-1)^2(2n-3)^2(2n-5)^2P_{2n-6}(0)=...=(-1)^n\prod\limits_{k=0}^{n-1}\(2n-(2k+1)\)^2)
Sauf erreurs de calculs...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 15:55
par pouik » 06 Jan 2007, 15:55
est-ce qu'un raisonnement comme le votre suffit, ou faut-il faire une récurrence ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 15:59
par tize » 06 Jan 2007, 15:59
Non, fais une récurrence, c'est plus sur...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 16:45
par pouik » 06 Jan 2007, 16:45
Montrons à présent ce résultat (
 = (-1)^n\displaystyle\prod_{k=0}^{n-1} (2n - (2k+1))^2)
) rigoureusement par une récurrence finie sur

.
Itération : Soit

.
- Supposons que :
 = (-1)^n\displaystyle\prod_{k=0}^{n-1} (2n - (2k+1))^2)
- Montrons que :
 = (-1)^n+1\displaystyle\prod_{k=0}^{n} (2(n+1) - (2k+1))^2) Itération :
Itération : D'après l'hypothèse de récurrence, on a la relation suivante :
 = (-1)^n\displaystyle\prod_{k=0}^{n-1} (2n - (2k+1))^2) Mais arrivé là je suis bloqué, je ne vois pas comment faire !!
Mais arrivé là je suis bloqué, je ne vois pas comment faire !!PS : J'ai un gros doute, je ne suis plus sur de savoir si la récurrence porte sur k ou sur n :doh: :doh: :doh:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 17:08
par tize » 06 Jan 2007, 17:08
Utilise
=-n^2P_{n-1}(0))
pour en déduire une relation simple de
)
en fonction de

...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 17:27
par pouik » 06 Jan 2007, 17:27
on a :
+1)} = -(2n+1)^2 P_{(2n+1)-1})
ie :
} = -(2n+1)^2 P_{2n})
Correct ??
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 17:31
par tize » 06 Jan 2007, 17:31
Oui, du coup :
= -(2n+1)^2 P_{2n}(0) = -(2n+1)^2.(-1)^n\displaystyle\prod_{k=0}^{n-1} (2n - (2k+1))^2)
Reste à montrer :
 = (-1)^{n+1}\displaystyle\prod_{k=0}^{n} (2(n+1) - (2k+1))^2)
pour achever la récurrence...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 17:38
par pouik » 06 Jan 2007, 17:38
sinon j'ai un problème pour faire l'initialisation : quand je pare de

, ca ne marche pas.


-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 17:45
par pouik » 06 Jan 2007, 17:45
sinon pour démontrer :
tize a écrit: = (-1)^{n+1}\displaystyle\prod_{k=0}^{n} (2(n+1) - (2k+1))^2)
j'avais songé à un changement d'indice mais a priori ca ne marche pas !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 17:47
par tize » 06 Jan 2007, 17:47
pouik a écrit:sinon j'ai un problème pour faire l'initialisation : quand je pare de

, ca ne marche pas.


Pour n=1on a

:
 = (-1)^1\displaystyle\prod_{k=0}^{0} (2 - (2k+1))^2 = -1)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 06 Jan 2007, 17:51
par pouik » 06 Jan 2007, 17:51
sinon qu'elle autre méthode me suggérez vous à la place du changement d'indidice qui ne semble pas foncyionner.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 06 Jan 2007, 17:56
par tize » 06 Jan 2007, 17:56
Tu ne vois donc pas que
 = (-1)^n\displaystyle\prod_{k=0}^{n-1} (2n - (2k+1))^2 = (-1)^n.1^2.3^2.5^2.....(2n-1)^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
