Décomposition en nombres premiers

[nodgim]

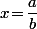
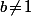
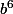
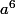
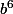
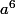
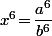
C'est quand même pas la mer à boire par contraposition : si est un rationnel non entier (sous forme irréductible), alors donc il existe premier qui divise et, évidement, qui ne divise pas donc divise mais pas et ça prouve que ne divise pas , c'est à dire que est non entier.
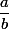
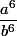
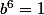
Sinon, tu peut aussi regarder directement la décomposition en facteurs premiers de et de qui n'ont aucun élément communs vu que est irréductible, et tu voit que est lui aussi sous forme irréductible donc entier ssi , c'est à dire .

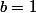
C'est sûr que ça se fait, mais il faut le faire, et du coup ça rallonge un peu la démo, non ?

[Ben314]

Oui, ça rallonge... si tu considère que le résultat n'est pas déjà connu (c'est quand même un truc archi. classique).

Et d'un autre coté, tu pourrait aussi supposer que le "théorème fondamental de l'arithmétique" (qui dit que tout entier se décompose de façon unique en produit de premier) n'est pas connu.
Et dans ce cas, la preuve de Doraki est plus courte vu que pour montrer le truc sur la puissance 6ème, il suffit d'avoir le lemme d'Euclide (si un premier divise un produit alors il divise l'un des termes du produit) et que le lemme d'Euclide se démontre plus rapidement que le théorème fondamental de l'arithmétique.
Enfin bref, comme souvent, la preuve "la plus rapide", ben ça dépend grandement de ce qu'on considère comme "connu" au départ.

[Pseuda]

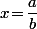
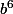
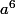
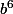
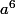
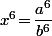
C'est quand même pas la mer à boire par contraposition : si est un rationnel non entier (sous forme irréductible), alors donc il existe premier qui divise et, évidement, qui ne divise pas donc divise mais pas et ça prouve que ne divise pas , c'est à dire que est non entier.
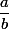
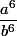
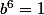
Sinon, tu peut aussi regarder directement la décomposition en facteurs premiers de et de qui n'ont aucun élément communs vu que est irréductible, et tu voit que est lui aussi sous forme irréductible donc entier ssi , c'est à dire .

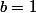
Bonjour,

Cette démonstration est bien compliquée. En démonstration directe :

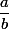
Soit fraction irréductible telle que . Alors, , donc , donc (car a et b premiers entre eux, avec le th. de Gauss), donc .

Par ailleurs, la décomposition en facteurs premiers est au programme du secondaire, tandis que celle-ci ne l'est pas.

[Abilys38]

Pardon mais je ne comprend pas ta démonstration pseuda.
Comment b peut diviser a si a et b sont premiers entre eux?

[nodgim]

Il y a le contexte du sujet, dont le titre est évocateur. La preuve par la décomposition me semble donc être celle, implicitement, qui est attendue. ça ne retire rien à la beauté de la preuve de Doraki.

[Pseuda]

Pardon mais je ne comprend pas ta démonstration pseuda.
Comment b peut diviser a si a et b sont premiers entre eux?

Et bien, avec b = 1.