Comparaison nombres premiers - idéaux premiers

par **Archimondain** » 18 Aoû 2010, 12:59

Bonjour,
je me pose la question de savoir ce qui justifie l'appellation de 'premier' pour un idéal.

C'est sans doute un peu naïf de ma part, mais on aurait eu

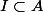
premier dans

un anneau

il n'existe aucun couple d'idéal

tel que

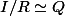
J'aurait tout de suite fait l'analogie

Au lieu de ça, on a juste

premier

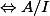
intègre. Là je reste sur ma faim...

Question subsidiaire, y-a-t-il une structure d'anneaux qui implique l'unicité de la décomposition de ses éléments en facteurs premiers ?

Merci pour vos réponses.

par **Nightmare** » 18 Aoû 2010, 13:15

Salut,

Tu peux montrer qu'un idéal I d'un anneau A est premier si et ssi, pour tous éléments x et y de A, si xy est dans I, alors l'un des deux, x ou y, est aussi dans I. On se rapproche déjà plus de la définition d'un nombre premier.

Concernant la décomposition unique en facteurs irréductible, les anneaux qui ont une telle structure sont appelés factoriels. Parmi eux, il y a par exemple tous les anneaux principaux. Je te laisse chercher de plus ample information sur le net.

par **lapras** » 18 Aoû 2010, 19:09

Salut,
pour moi la manière la plus logique de comprendre la notion d'idéal "premier" est la suivante (dans un anneau de Dedekind):
I est premier <=> tout idéal divisant I (A divise I <=> il existe B tel que I = AB <=> I contenu dans A) est I ou l'anneau entier.

par **Finrod** » 18 Aoû 2010, 19:48

Pourquoi prendre un anneau de Dedekind ?

La notion d'idéal premier donne bien ce genre de chose même dans un monoïde.

par **lapras** » 18 Aoû 2010, 19:51

Je ne sais pas trop, je ne travaille que dans des idéaux d'un anneau de corps de nombre,
mais penses tu que dans un anneau quelconque, A divise B <=> B contenu dans A ?

par **Archimondain** » 18 Aoû 2010, 19:53

Merci !
Cette vision des choses éclaire pour moi beaucoup de choses.
Une confusion que j'ai vient sans doute du fait que I/C isomorphe à B n'est pas équivalent à I isomorphe à BC.

@Nightmare
Je vais regarder les anneaux factoriels. Mais une question me vient. Pourquoi aurait-on besoin d'une structure d'anneaux pour définir la décomposition en facteurs premiers ? Une structure de groupe ne devrait-elle pas suffire ?

par **Nightmare** » 18 Aoû 2010, 19:57

Qu'appelle-t-on élément "premier" dans un groupe?

par **Archimondain** » 18 Aoû 2010, 20:50

Hum...
Ben je dirais

premier ssi quelque soit (a,b) dans G, a+b=x implique a=0 et b=x (ou vice-versa).

Ajout :
Ouai, bon, c'est un peu foireux en fait, vu que (Z,*) n'est pas un groupe...

par **Doraki** » 18 Aoû 2010, 20:58

Bah ça va être dur d'être premier vu que pour n'importe quel y dans G, x = (x-y) + y.
A part les groupes à 1 ou 2 éléments, j'vois pas beaucoup de candidats.

A la limite on peut dire que (A,+,*) admet la décomposition unique en facteurs premiers <=> (A*, *) est un monoïde libre.

par **Archimondain** » 18 Aoû 2010, 21:10

Ben d'une certaine manière x = (x-y) + y c'est aussi x = x + (-y+y) -> x = x + 0
Evidemment ma définition ne prend pas ça en compte.

Ba de toute façon je pense pas que ce soit très intéressant. Je vais potasser mes bouquins et me poser des questions existentielles plus tard :)

par **Finrod** » 18 Aoû 2010, 23:59

Nightmare a écrit:Qu'appelle-t-on élément "premier" dans un groupe?

Je note G le groupe.
Je dirais que ton elt premier est le générateur d'un idéal principal premier. Sachant qu'un G-module est u ensemble muni d'une action de G et qu'un idéal de G est un sous-G-module de G.

par **Finrod** » 19 Aoû 2010, 00:08

lapras a écrit:Je ne sais pas trop, je ne travaille que dans des idéaux d'un anneau de corps de nombre,
mais penses tu que dans un anneau quelconque, A divise B B contenu dans A ?

Un sens est évident. L'autre... je suis sur qu'on peut trouver un contre exemple.

Vu que j'ai déjà travaillé avec juste des relations d'inclusion et que ça marche bien, je dirais que ce n'est pas un drame s'il faut une hypothèse en plus.

par **lapras** » 19 Aoû 2010, 01:21

En fait quand tu n'est pas dans un anneau "cool" tu ne fais pas vraiment de l'arithmétique avec des idéaux je pense. (dans un anneau de dedekind on a la décomposition d'idéal en idéaux premiers)

par **Finrod** » 19 Aoû 2010, 08:42

Dans le cas le plus général, tu as toujours que l'ensemble des idéaux est un monoïde pour le produit d'idéaux.

En regardant ses sous-monoïdes et en ajoutant deux conditions simples, une de finitude et une qui imite la régularité par rapport à la division, on retrouve des ensembles d'idéaux qui caractérisent la topologie de Zariski de l'anneau.

Plus précisément, si on se fixe un tel monoïde, l'ensemble des idéaux premier qu'il contient est un fermé Zariski de A.

C'est amusant de voir que c'est lié.

Comparaison nombres premiers - idéaux premiers

Comparaison nombres premiers - idéaux premiers

Qui est en ligne