(Z/nZ)*et decomposition en facteurs de n

[RadarX]

Respects a tous,

Si n = p1^a1...pr^ar (decomposition en facteurs premiers), alors (Z/nZ)* est isomorphe a (Z/p1^a1Z)* X ... X (Z/pr^arZ)*.
Je le prouve facilement ainsi:
(Z/nZ)* = [Z/(p1^a1...pr^ar)Z]* ~ (Z/(p1^a1)Z)* X ... X (Z/(pr^ar)Z)* =
[Z/p1^a1Z]* X ... X [Z/pr^arZ]* .

En fait cela decoule du fait que (G X H)* = G* X H*!!!

Voyez vous alors un bug dans cette petite preuve? Je soumets ce probleme car j'ai vu une autre preuve dans la litterature qui utilise l'isomorphisme
Aut(Z/nZ) ~ (Z/nZ)* je trouve ca un peu... maso!

Merci!

[thomasg]

bonjour,

si il y a un manque dans ta preuve, c'est lorsque tu utilises le premier isomorphisme.

Si tu peux détailler ce point simplement, ta preuve semble bonne.

A plus.

(de vagues souvenirs de mes cours, me font dire que la preuve n'est pourtant pas évidente.)

[phenomene]

Cela m'a l'air d'aller : est isomorphe à en vertu du théorème chinois, puis on peut en effet utiliser le fait que le groupe des inversibles d'un groupe produit est le produit des groupes des inversibles de chaque facteur, bref, on peut ajouter des petites étoiles partout.

[Galt]

Inversibles d'un groupe ? Il s'agit malheureusement des inversibles d'un anneau.
Je suis en train de regarder si l'isomorphisme chinois est bien un isomorphisme d'anneaux (ça marche avec 2 et 3)

[phenomene]

Oups, j'ai dit n'importe quoi ! :marteau: Merci Galt.

[phenomene]

L'isomorphisme chinois est bien un isomorphisme d'anneaux, non ? Bon, ça ne m'excuse pas pour avoir écrit n'importe quoi bien sûr.

[Galt]

C'est bien un isomorphisme d'anneaux, et je le prouve.
Soit p et q deux entiers premiers entre eux, avec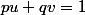 et définie par l'isomorphisme chinois (de groupes pour l'instant). On doit comparer avec (modulo pq).

(puisqu'on travaille modulo pq )
Donc

(je rappelle que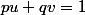 et qu'on travaille modulo )
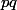Et voila
La boucle est bouclée

[RadarX]

Merci a tous pour le contributions;
j'aurais du précisé que j'utilisais le theoreme chinois dans les anneaux (et aurais meme pu le demontrer) pour mon premier isomorphisme.

Vos avis me rassurent, mais comme thomasg, moi aussi, de vieux souvenirs de cours ajoutés a la preuve que j'ai sous les mains entretiennent le doute d'une subtilité qui m'aurait échappée.

Encore merci.
Je file quand meme la preuve qui me fait douter

On a d'abord une preuve prealable de l'isomorphisme (Z/nZ)* ~ Aut (Z/nZ)
Ensuite le lemme Chinois ==> Z/nZ ~ Z/(p1^a1)Z X ... X Z/(pr^ar)Z
et le resultat decoule du fait que cet isomorphisme induit cet autre
Aut (Z/nZ) ~ Aut (Z/(p1^a1)Z) X ... X Aut (Z/(pr^ar)Z).
En effet soit f € Aut(Z/nZ); f est caracterisé par f(1). Par l'isomorphisme donné par le lemme chinois, 1 s'envoie sur (1, ... , 1). Notons ei = (0,...,0,1,0...,0), il suffit alors de monter que f(ei) € au sous groupe engendré par ei. Or (pi^ai)ei = 0 donc (pi^ai)f(ei) de sorte que f(ei) est d'ordre une puissance de pi, d'ou le resultat.!!?????