Décomposition en facteurs irréductibles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Mai 2012, 12:31
par barbu23 » 10 Mai 2012, 12:31
Bonjour à tous,
D'après le théorème fondamental de l'algèbre, un polynôme de degré

sur
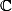
:
 = a_{n} x^n + a^{n-1} x^{n-1} + ... + a_1 x + a_0 $)
admet une décomposition de la forme :
 = a_{n} ( x - \lambda_{1} ) ( x - \lambda_{2} ) ... ( x - \lambda_{n} ) $)
.
Pourriez vous me dire comme on fait pour démontrer qu'une telle décomposition est unique ?
C'est à dire, s'il existe deux décompositions pour

de la forme :
 = ( x - \alpha_{1} ) ( x - \alpha_{2} ) ... ( x - \alpha_{n}) = ( x - \beta_{1} ) ( x - \beta_{2} ) ... ( x - \beta_{n}) $)
, alors, il existe
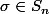
( groupe des permutations ) telle que :
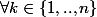
:
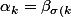 } $)
.
Merci d'avance.
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 10 Mai 2012, 12:43
par gdlrdc » 10 Mai 2012, 12:43
Bonjour,
S'il existe un beta qui n'appartient pas à l'ensemble des alpha alors P admet au moins n+1 racines ce qui est impossible vu que P est de degré n.
ça te va comme explication?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 10 Mai 2012, 17:13
par leon1789 » 10 Mai 2012, 17:13
barbu23 a écrit:  = ( x - \alpha_{1} ) ( x - \alpha_{2} ) ... ( x - \alpha_{n}) = ( x - \beta_{1} ) ( x - \beta_{2} ) ... ( x - \beta_{n}) $)
,
évalue
 = ( x - \alpha_{1} ) ( x - \alpha_{2} ) ... ( x - \alpha_{n}))
en
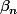
et utilise que, dans C, un produit est nul si et seulement si l'un des termes est nul.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités